Hypersurface
A generalization of the concept of an ordinary surface in three-dimensional space to the case of an  -dimensional space. The dimension of a hypersurface is one less than that of its ambient space.
-dimensional space. The dimension of a hypersurface is one less than that of its ambient space.
If 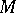 and
and 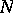 are differentiable manifolds,
are differentiable manifolds, 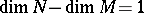 , and if an immersion
, and if an immersion 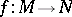 has been defined, then
has been defined, then 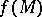 is a hypersurface in
is a hypersurface in 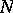 . Here
. Here 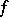 is a differentiable mapping whose differential
is a differentiable mapping whose differential 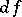 at any point
at any point 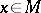 is an injective mapping of the tangent space
is an injective mapping of the tangent space 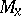 to
to 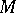 at
at  into the tangent space
into the tangent space 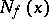 to
to 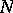 at
at 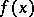 .
.
Comments
References
| [a1] | M. Spivak, "A comprehensive introduction to differential geometry" , 1979 , Publish or Perish (1975) pp. 1–5 |
An algebraic hypersurface is a subvariety of an algebraic variety that is locally defined by one equation. An algebraic hypersurface in the affine space 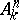 over a field
over a field 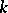 is globally defined by one equation
is globally defined by one equation
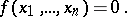 |
An algebraic hypersurface 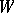 in a projective space
in a projective space 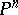 is defined by an equation
is defined by an equation
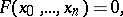 |
where 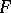 is a homogeneous form in
is a homogeneous form in 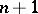 variables. The degree
variables. The degree 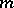 of this form is said to be the degree (order) of the hypersurface. A closed subscheme
of this form is said to be the degree (order) of the hypersurface. A closed subscheme 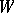 of a scheme
of a scheme 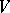 is said to be a hypersurface if the corresponding sheaf of ideals
is said to be a hypersurface if the corresponding sheaf of ideals 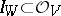 is a sheaf of principal ideals. For a connected non-singular algebraic variety this condition means that the codimension of
is a sheaf of principal ideals. For a connected non-singular algebraic variety this condition means that the codimension of 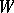 in
in 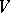 is one. For each non-singular algebraic hypersurface
is one. For each non-singular algebraic hypersurface 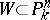 of order
of order 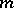 (often denoted by
(often denoted by 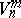 ) the following holds:
) the following holds:
a) the canonical class 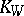 is equal to
is equal to 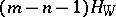 where
where 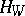 is the class of a hyperplane section of
is the class of a hyperplane section of 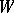 ;
;
b) the cohomology groups 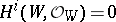 for
for 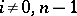 , and
, and
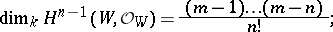 |
c) if 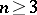 , the fundamental group (algebraic or topological if
, the fundamental group (algebraic or topological if 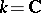 )
) 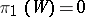 ;
;
d) if 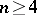 , the Picard group
, the Picard group 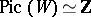 and is generated by the class of a hyperplane section.
and is generated by the class of a hyperplane section.
I.V. Dolgachev
Comments
The cohomology ring of a smooth complex projective hypersurface can be expressed completely in terms of rational differential forms on the ambient projective space, [a1]. In most cases, the period mapping for these hypersurfaces has been shown to be of degree one [a2].
References
| [a1] | J. Carlson, P. Griffiths, "Infinitesimal variations of Hodge structure and the global Torelli problem" A. Beauville (ed.) , Algebraic geometry (Angers, 1979) , Sijthoff & Noordhoff (1980) pp. 51–76 |
| [a2] | R. Donagi, "Generic Torelli for projective hypersurfaces" Compos. Math. , 50 (1983) pp. 325–353 |
| [a3] | R. Hartshorne, "Algebraic geometry" , Springer (1977) pp. 13; 170; 316; 381 |
An analytic hypersurface is a set 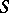 in a complex Euclidean space
in a complex Euclidean space 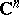 that, in a neighbourhood of each of its points
that, in a neighbourhood of each of its points 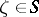 , is defined by an equation
, is defined by an equation 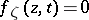 , where the function
, where the function 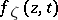 is continuous with respect to the parameter
is continuous with respect to the parameter 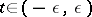 ,
, 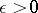 , and, for each fixed
, and, for each fixed 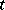 , is holomorphic in
, is holomorphic in  in a neighbourhood
in a neighbourhood 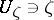 which is independent of
which is independent of 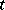 ; moreover,
; moreover, 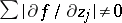 for all
for all 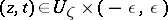 . In other words, an analytic hypersurface is a set in
. In other words, an analytic hypersurface is a set in 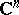 that is locally the union of a continuous one-parameter family of complex-analytic surfaces of complex codimension one. For instance, if a function
that is locally the union of a continuous one-parameter family of complex-analytic surfaces of complex codimension one. For instance, if a function 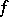 is holomorphic in a domain
is holomorphic in a domain 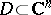 and
and 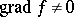 in
in 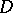 , then the sets
, then the sets 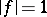 ,
, 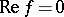 , etc., are analytic hypersurfaces.
, etc., are analytic hypersurfaces.
A twice-differentiable hypersurface 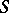 in
in 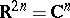 is an analytic hypersurface if and only if its Levi form vanishes identically on
is an analytic hypersurface if and only if its Levi form vanishes identically on 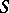 or if
or if 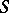 is locally pseudo-convex on both sides.
is locally pseudo-convex on both sides.
E.M. Chirka
Comments
Sometimes the phrase "analytic hypersurface" is also used for an analytic set of complex codimension 1, analogously to 3) above, cf. [a1]. An analytic hypersurface as in 4) is also called a foliation by analytic varieties of codimension 1. The result concerning a twice-differentiable 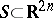 , mentioned above, can be found in [a2].
, mentioned above, can be found in [a2].
References
| [a1] | H. Grauert, R. Remmert, "Theory of Stein spaces" , Springer (1977) (Translated from German) |
| [a2] | V.S. Vladimirov, "Methods of the theory of functions of several complex variables" , M.I.T. (1966) (Translated from Russian) |
| [a3] | L. Kaup, B. Kaup, "Holomorphic functions of several variables" , de Gruyter (1983) (Translated from German) |
Hypersurface. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Hypersurface&oldid=14567