Real-analytic space
An analytic space over the field 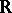 of real numbers. Unlike in the case of complex-analytic spaces, the structure sheaves of real-analytic spaces need not be coherent (cf. Coherent sheaf). Real-analytic spaces are said to be coherent if their structure sheaves are coherent. All real-analytic manifolds (i.e. smooth real-analytic spaces) are coherent real-analytic spaces.
of real numbers. Unlike in the case of complex-analytic spaces, the structure sheaves of real-analytic spaces need not be coherent (cf. Coherent sheaf). Real-analytic spaces are said to be coherent if their structure sheaves are coherent. All real-analytic manifolds (i.e. smooth real-analytic spaces) are coherent real-analytic spaces.
Let 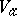 be the germ at a point
be the germ at a point  of a real-analytic subset of
of a real-analytic subset of 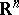 (cf. Analytic set). This defines the germ at
(cf. Analytic set). This defines the germ at  of a complex-analytic subset
of a complex-analytic subset 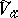 of the space
of the space 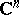 with the following equivalent properties: 1)
with the following equivalent properties: 1) 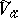 is the intersection of all germs of complex-analytic sets containing
is the intersection of all germs of complex-analytic sets containing 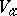 ; 2) if
; 2) if 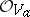 is the analytic algebra of the germ
is the analytic algebra of the germ 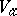 , then
, then 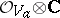 is the analytic algebra of the germ
is the analytic algebra of the germ 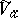 . The germ
. The germ 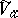 is said to be the complexification of the germ
is said to be the complexification of the germ 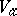 , and
, and 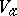 is said to be the real part of the germ
is said to be the real part of the germ 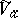 . Analogously, for any coherent real-analytic countably-infinite space
. Analogously, for any coherent real-analytic countably-infinite space 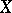 it is possible to construct the complexification
it is possible to construct the complexification  , which is a complex-analytic space.
, which is a complex-analytic space. 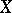 will then have a fundamental system of neighbourhoods in
will then have a fundamental system of neighbourhoods in 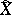 which are Stein spaces (cf. Stein space).
which are Stein spaces (cf. Stein space).
The theory of coherent real-analytic spaces is similar to the theory of complex Stein spaces. Global sections of any coherent analytic sheaf of modules 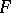 on a coherent real-analytic countably-infinite space
on a coherent real-analytic countably-infinite space 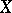 generate modules of germs of its sections at any point of
generate modules of germs of its sections at any point of 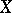 , and all groups
, and all groups 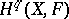 vanish if
vanish if 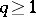 .
.
For any finite-dimensional coherent real-analytic countably-infinite space 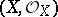 there exists a morphism
there exists a morphism
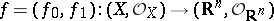 |
such that 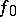 is a proper one-to-one mapping of
is a proper one-to-one mapping of 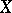 into a coherent subspace in
into a coherent subspace in 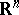 , while
, while 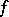 is an imbedding at the smooth points of
is an imbedding at the smooth points of 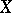 . In particular, any (Hausdorff and countably-infinite) real-analytic manifold is isomorphic to a real-analytic submanifold in
. In particular, any (Hausdorff and countably-infinite) real-analytic manifold is isomorphic to a real-analytic submanifold in 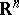 . For a reduced coherent real-analytic space
. For a reduced coherent real-analytic space 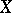 the set of classes of isomorphic real-analytic principal fibre bundles with a real structure Lie group
the set of classes of isomorphic real-analytic principal fibre bundles with a real structure Lie group 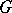 , admitting complexification, and base
, admitting complexification, and base 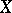 is in one-to-one correspondence with the set of classes of isomorphic topological principal fibre bundles with the same structure group
is in one-to-one correspondence with the set of classes of isomorphic topological principal fibre bundles with the same structure group 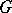 .
.
References
| [1] | A. Tognoli, "Some results in the theory of real analytic spaces" M. Jurchesan (ed.) , Espaces Analytiques (Bucharest 1969) , Acad. Roumanie (1971) pp. 149–157 |
Comments
References
| [a1] | H. Cartan, "Variétés analytiques réelles et variétés analytiques complexes" Bull. Soc. Math. France , 85 (1957) pp. 77–99 |
| [a2] | F. Bruhat, H. Cartan, "Sur la structure des sous-ensembles analytiques réels" C.R. Acad. Sci. Paris , 244 (1957) pp. 988–900 |
| [a3] | F. Bruhat, H. Cartan, "Sur les composantes irréductibles d'un sous-ensemble" C.R. Acad. Sci. Paris , 244 (1957) pp. 1123–1126 |
| [a4] | F. Bruhat, H. Whitney, "Quelques propriétés fondamentales des ensembles analytiques-réels" Comm. Math. Helv. , 33 (1959) pp. 132–160 |
| [a5] | R. Narasimhan, "Introduction to the theory of analytic spaces" , Lect. notes in math. , 25 , Springer (1966) |
| [a6] | H. Grauert, R. Remmert, "Theory of Stein spaces" , Springer (1979) (Translated from German) |
Real-analytic space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Real-analytic_space&oldid=14527