Space with an indefinite metric
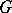 -space
-space
A pair of objects 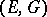 , the first of which is a vector space
, the first of which is a vector space 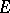 over the field of complex numbers, while the second is a bilinear (more precisely, sesquilinear) form
over the field of complex numbers, while the second is a bilinear (more precisely, sesquilinear) form 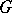 on
on 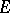 ; this form is also called a
; this form is also called a  -metric. If
-metric. If 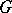 is a positive-definite (a so-called definite) form, then it is a scalar product in
is a positive-definite (a so-called definite) form, then it is a scalar product in  , and one can use it to canonically introduce (cf., e.g., Hilbert space with an indefinite metric) a norm and a distance (i.e. an ordinary metric) for the elements of
, and one can use it to canonically introduce (cf., e.g., Hilbert space with an indefinite metric) a norm and a distance (i.e. an ordinary metric) for the elements of 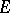 . In the case of a general sesquilinear form
. In the case of a general sesquilinear form 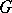 there is neither a norm nor a metric canonically related to
there is neither a norm nor a metric canonically related to  , and the phrase "G-metric" only recalls the close relation of definite sesquilinear forms with certain metrics in vector spaces.
, and the phrase "G-metric" only recalls the close relation of definite sesquilinear forms with certain metrics in vector spaces.
The theory of finite-dimensional spaces with an indefinite metric, more often called bilinear metric spaces, or spaces with a bilinear metric, was developed already by G. Frobenius, and is expounded in courses on linear algebra (cf. [1]).
The main purpose of the general theory of spaces with an indefinite metric is the separation and study of relatively simple, but for applications important, classes of non-self-adjoint operators in a Hilbert space (cf. Non-self-adjoint operator). Spaces with an indefinite metric were for the first time introduced by L.S. Pontryagin [2] (for more detail, see Pontryagin space).
The theory of spaces with an indefinite metric has been developed in two directions — their geometry and linear operations on them.
In the geometry of spaces with an indefinite metric one basically studies: a) the relation between the 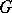 -metric and various topologies on
-metric and various topologies on 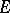 ; b) the classification of vector subspaces (linear manifolds) in
; b) the classification of vector subspaces (linear manifolds) in 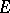 relative to the
relative to the 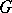 -metric (especially, the so-called definite subspaces, see below); c) the properties of
-metric (especially, the so-called definite subspaces, see below); c) the properties of  -projections; and d) bases of
-projections; and d) bases of 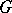 -spaces.
-spaces.
In the case of a Hermitian 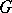 -metric (a
-metric (a 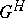 -metric), i.e. such that
-metric), i.e. such that  for all
for all 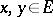 , the most important results and concepts in the geometry of spaces with an indefinite metric are as follows. Suppose that each vector
, the most important results and concepts in the geometry of spaces with an indefinite metric are as follows. Suppose that each vector 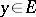 is put in correspondence with a linear functional
is put in correspondence with a linear functional 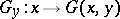 ,
, 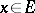 . A topology
. A topology  on
on 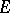 is called subordinate to the
is called subordinate to the 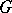 -metric if
-metric if 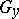 is continuous in
is continuous in  for all
for all 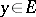 ;
;  is called compatible with the
is called compatible with the 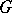 -metric if it is subordinate to
-metric if it is subordinate to 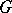 and if every
and if every  -continuous functional has the form
-continuous functional has the form 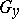 ,
,  . In a space
. In a space 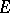 with an indefinite metric one cannot specify more than one Fréchet topology subordinate to
with an indefinite metric one cannot specify more than one Fréchet topology subordinate to 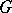 , and not every
, and not every 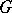 -metric allows such a topology (cf. [4]). If a topology, subordinate to the
-metric allows such a topology (cf. [4]). If a topology, subordinate to the  -metric, is a pre-Hilbert topology on
-metric, is a pre-Hilbert topology on 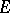 and is given by a scalar product
and is given by a scalar product 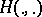 in
in  , then
, then 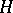 is called a Hermitian non-negative majorant of
is called a Hermitian non-negative majorant of 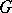 ; in this case
; in this case
 |
After completing in the 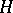 -norm one obtains a Hilbert space with indefinite metric
-norm one obtains a Hilbert space with indefinite metric 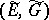 , where
, where 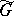 is the continuous extension of
is the continuous extension of  to the entire space
to the entire space 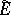 . Here,
. Here, 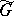 may turn out to be a degenerate metric, even if
may turn out to be a degenerate metric, even if 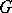 is non-degenerate. This degeneration does not occur if
is non-degenerate. This degeneration does not occur if 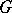 is a non-degenerate metric and if the largest of the dimensions
is a non-degenerate metric and if the largest of the dimensions 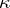 of the positive subspaces of
of the positive subspaces of 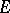 is finite. In the latter case one obtains the Pontryagin space
is finite. In the latter case one obtains the Pontryagin space 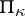 .
.
A subspace 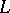 in a space
in a space 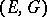 with an indefinite metric is called a positive subspace, a negative subspace (a more general name is: a definite subspace) or a neutral subspace, depending on whether
with an indefinite metric is called a positive subspace, a negative subspace (a more general name is: a definite subspace) or a neutral subspace, depending on whether 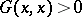 ,
, 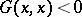 or
or 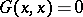 for all
for all 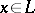 . A subspace is called maximally positive if it is positive and cannot be extended with preservation of this property. Every subspace of the type indicated above is contained in a maximal subspace of the same type.
. A subspace is called maximally positive if it is positive and cannot be extended with preservation of this property. Every subspace of the type indicated above is contained in a maximal subspace of the same type.
An important part in the classification of subspaces in spaces with an indefinite metric is played by the notions of a canonical decomposition and a 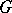 -orthogonal projection.
-orthogonal projection.
A vector 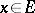 is called
is called 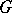 -orthogonal to a subspace
-orthogonal to a subspace 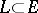 (is isotropic with respect to
(is isotropic with respect to  ) if
) if  for all
for all 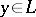 . A subspace
. A subspace  is called degenerate if it contains at least one non-zero vector that is isotropic with respect to
is called degenerate if it contains at least one non-zero vector that is isotropic with respect to 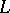 .
.
If 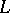 is a subspace in a space
is a subspace in a space  with an indefinite metric, then
with an indefinite metric, then  is its
is its 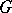 -orthogonal complement. Always
-orthogonal complement. Always 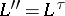 , where
, where  is any topology compatible with
is any topology compatible with 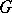 . The
. The  -orthogonal complement
-orthogonal complement 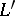 of a degenerate vector subspace
of a degenerate vector subspace 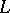 is a degenerate vector subspace that is closed in a topology
is a degenerate vector subspace that is closed in a topology  compatible with
compatible with 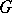 , and
, and 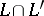 is the vector subspace of isotropic elements. A subspace
is the vector subspace of isotropic elements. A subspace 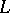 is called projection complete if each
is called projection complete if each 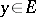 has a
has a 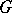 -projection on
-projection on 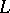 , i.e. if there is an
, i.e. if there is an  for which
for which 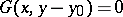 for every
for every 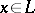 . Uniqueness of a
. Uniqueness of a 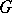 -projection on
-projection on 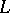 is equivalent with
is equivalent with  being a non-degenerate subspace, while its existence depends on the continuity of the functional
being a non-degenerate subspace, while its existence depends on the continuity of the functional 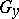 in topologies on
in topologies on 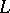 compatible with
compatible with 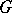 . If
. If 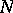 and
and  are
are 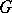 -orthogonal subspaces and
-orthogonal subspaces and 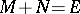 , then
, then 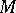 and
and 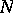 are projection complete; if
are projection complete; if 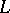 is a projection-complete subspace, then
is a projection-complete subspace, then 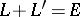 ; the sum is the direct sum if
; the sum is the direct sum if 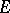 is a non-degenerate space with an indefinite metric.
is a non-degenerate space with an indefinite metric.
Suppose that  is a definite subspace in a space with an indefinite metric
is a definite subspace in a space with an indefinite metric 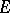 . It is called regular if every functional
. It is called regular if every functional 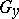 ,
, 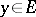 , is continuous on
, is continuous on 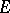 in the norm
in the norm 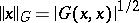 . Otherwise it is called singular. Every non-degenerate infinite-dimensional space with an indefinite metric contains singular subspaces. A definite subspace
. Otherwise it is called singular. Every non-degenerate infinite-dimensional space with an indefinite metric contains singular subspaces. A definite subspace 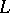 is projection complete if and only if it is regular and if for every
is projection complete if and only if it is regular and if for every 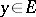 there is an
there is an 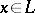 such that
such that
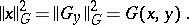 |
Linear operators in spaces with an indefinite metric have been studied mainly in Hilbert spaces with an indefinite metric; for Banach analogues there is a survey in [8].
As in the case of Hilbert spaces with an indefinite metric, an important tool in the study of the geometry of spaces with an indefinite metric and of linear operators in spaces 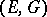 endowed with some topology compatible with
endowed with some topology compatible with 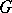 , are the so-called
, are the so-called 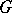 -orthogonal bases in
-orthogonal bases in 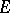 , i.e. bases
, i.e. bases 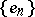 of the topological vector space
of the topological vector space 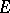 for which
for which  ,
, 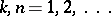 (cf. [4]).
(cf. [4]).
References
| [1] | A.I. Mal'tsev, "Foundations of linear algebra" , Freeman (1963) (Translated from Russian) |
| [2] | L.S. Pontryagin, "Hermitian operators in spaces with indefinite metric" Izv. Akad. Nauk SSSR Ser. Mat. , 8 (1944) pp. 243–280 (In Russian) |
| [3] | I.S. Iokhvidov, M.G. Krein, "Spectral theory in spaces with an indefinite metric I" Transl. Amer. Math. Soc. , 13 (1960) pp. 105–176 Trudy Moskov. Mat. Obshch. , 5 (1956) pp. 367–432 |
| [4] | Yu.P. Ginzburg, I.S. Iokhvidov, "The geometry of infinite-dimensional spaces with a bilinear metric" Russian Math. Surveys , 17 : 4 (1962) pp. 1–51 Uspekhi Mat. Nauk , 17 : 4 (1962) pp. 3–56 |
| [5] | M.G. Krein, "Introduction to the geometry of indefinite 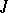 -spaces and the theory of operators in these spaces" , Second Math. Summer School , 1 , Kiev (1965) pp. 15–92 (In Russian) -spaces and the theory of operators in these spaces" , Second Math. Summer School , 1 , Kiev (1965) pp. 15–92 (In Russian) |
| [6] | T.Ya. Azizov, I.S. Iokhvidov, "Linear operators in Hilbert spaces with 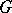 -metric" Russian Math. Surveys , 26 : 4 (1971) pp. 45–97 Uspekhi Mat. Nauk , 26 : 4 (1971) pp. 43–92 -metric" Russian Math. Surveys , 26 : 4 (1971) pp. 45–97 Uspekhi Mat. Nauk , 26 : 4 (1971) pp. 43–92 |
| [7] | K.L. Nagy, "State vector spaces with indefinite metric in quantum field theory" , Noordhoff (1966) |
| [8] | I.S. Iokhvidov, "Banach spaces with a 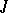 -metric and certain classes of linear operators in these spaces" Izv. Akad. Nauk MoldavSSR , 1 (1968) pp. 60–80 (In Russian) -metric and certain classes of linear operators in these spaces" Izv. Akad. Nauk MoldavSSR , 1 (1968) pp. 60–80 (In Russian) |
Comments
A topology  that is compatible with the
that is compatible with the 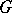 -metric is also called an admissible topology. For an admissible topology,
-metric is also called an admissible topology. For an admissible topology, 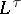 denotes the
denotes the  -closure of
-closure of 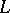 in
in 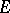 . The
. The  -orthogonal complement is called the orthogonal companion in [a2]. The weak topology on the
-orthogonal complement is called the orthogonal companion in [a2]. The weak topology on the 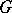 -space
-space 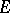 is the locally convex topology defined by the family of semi-norms (cf. Semi-norm)
is the locally convex topology defined by the family of semi-norms (cf. Semi-norm)
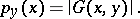 |
It is an admissible topology, and the weakest such. As a consequence of the double orthogonal complement theorem,  , one thus has that
, one thus has that 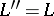 if and only if
if and only if 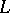 is weakly closed.
is weakly closed.
For additional information about spaces with an indefinite metric see Krein space and [a1]–[a4].
References
| [a1] | T.Ya. Azizov, I.S. [I.S. Iokhvidov] Iohidov, "Linear operators in spaces with an indefinite metric" , Wiley (1989) (Translated from Russian) |
| [a2] | J. Bognár, "Indefinite inner product spaces" , Springer (1974) |
| [a3] | I. [I. Gokhberg] Gohberg, P. Lancaster, L. Rodman, "Matrices and indefinite scalar products" , Birkhäuser (1983) |
| [a4] | I.S. [I.S. Iokhvidov] Iohidov, M.G. Krein, H. Langer, "Introduction to the spectral theory of operators in spaces with an indefinite metric" , Akademie Verlag (1982) |
Space with an indefinite metric. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Space_with_an_indefinite_metric&oldid=14519