Principal G-object
in a category
A concept in the theory of categories, instances of which are a principal fibre bundle in topology, a principal homogeneous space in algebraic geometry, etc. Let 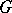 be a group object in a category
be a group object in a category 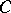 with products and final object
with products and final object  . An object
. An object 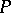 is said to be a
is said to be a 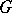 -object if there is given a morphism
-object if there is given a morphism  for which the following diagrams are commutative:
for which the following diagrams are commutative:
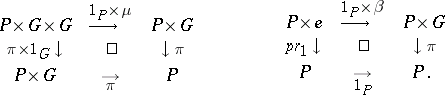 |
Here  is the group law morphism on
is the group law morphism on 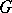 , while
, while 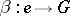 is the unit element morphism into
is the unit element morphism into 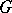 . More precisely, the
. More precisely, the 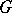 -objects specified as above are called right
-objects specified as above are called right 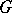 -objects; the definition of left
-objects; the definition of left 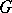 -objects is similar. As an example of a
-objects is similar. As an example of a 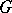 -object one may take the group object
-object one may take the group object 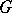 itself, for which
itself, for which 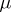 coincides with
coincides with 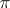 . This object is called the trivial
. This object is called the trivial 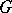 -object. The
-object. The 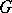 -objects in the category
-objects in the category 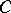 form a category
form a category 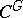 . The morphisms are morphism
. The morphisms are morphism  of
of 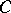 which commute with
which commute with 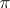 (i.e. such that
(i.e. such that 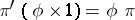 ). A
). A 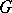 -object is said to be a formal principal
-object is said to be a formal principal  -object if the morphisms
-object if the morphisms  and
and 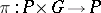 induce an isomorphism
induce an isomorphism 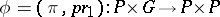 . If
. If 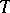 is some Grothendieck topology on the category
is some Grothendieck topology on the category 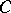 , a formal principal
, a formal principal 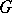 -object
-object 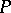 is called a principal
is called a principal 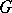 -object (with respect to the topology
-object (with respect to the topology 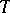 ) if there exists a covering
) if there exists a covering 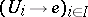 of the final object such that for any
of the final object such that for any 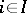 the product
the product 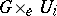 is isomorphic to the trivial
is isomorphic to the trivial 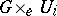 -object.
-object.
Examples.
1) If 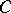 is the category of sets and
is the category of sets and 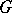 is a group, then the non-empty
is a group, then the non-empty 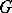 -objects are called
-objects are called 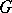 -sets. These are sets
-sets. These are sets 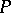 for which a mapping
for which a mapping 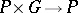 (
(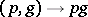 ) is defined such that for any
) is defined such that for any 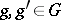 one has
one has 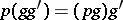 , and for any
, and for any 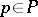 it is true that
it is true that  . A principal
. A principal 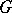 -object is a
-object is a 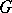 -set in which for any
-set in which for any 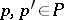 there exists a unique element
there exists a unique element 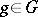 such that
such that 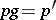 (a principal homogeneous
(a principal homogeneous 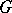 -set). If
-set). If 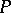 is not empty, the choice of a
is not empty, the choice of a 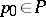 determines a mapping
determines a mapping 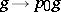 which establishes an isomorphism between
which establishes an isomorphism between 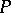 and the trivial
and the trivial 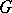 -set
-set 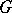 . Thus, in any topology a formal principal
. Thus, in any topology a formal principal 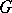 -object is a principal
-object is a principal 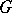 -object.
-object.
2) If 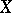 is a differentiable manifold and
is a differentiable manifold and 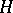 is a Lie group, then, taking
is a Lie group, then, taking 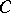 to be the category of fibrations over
to be the category of fibrations over 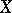 , taking as group object
, taking as group object 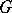 the projection
the projection 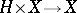 , and defining a topology in
, and defining a topology in 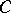 with the aid of families of open coverings, it is possible to obtain the definition of a principal
with the aid of families of open coverings, it is possible to obtain the definition of a principal 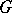 -fibration.
-fibration.
If 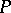 is a formal principal
is a formal principal 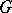 -object in a category
-object in a category 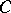 , then for any object
, then for any object 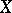 in the category
in the category 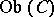 the set
the set 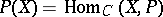 is either empty or is a principal homogeneous
is either empty or is a principal homogeneous 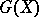 -set.
-set.
A formal principal 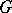 -object
-object 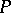 is isomorphic to the trivial
is isomorphic to the trivial 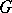 -object if and only if there exists a section
-object if and only if there exists a section 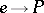 . The set of isomorphism classes of formal principal
. The set of isomorphism classes of formal principal 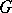 -objects is denoted by
-objects is denoted by 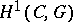 . If
. If 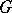 is an Abelian group object, then the set
is an Abelian group object, then the set 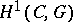 , with the class of trivial
, with the class of trivial  -objects as a base point, is a group and can be computed by standard tools of homological algebra. In general, in the computation of
-objects as a base point, is a group and can be computed by standard tools of homological algebra. In general, in the computation of 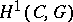 Čech homology constructions are employed (cf. Non-Abelian cohomology).
Čech homology constructions are employed (cf. Non-Abelian cohomology).
References
| [1] | A. Grothendieck (ed.) et al. (ed.) , Revêtements étales et groupe fondamental. SGA 1 , Lect. notes in math. , 224 , Springer (1971) |
Comments
Formal principal 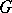 -objects are commonly called
-objects are commonly called 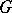 -torsors. The distinction between formal principal
-torsors. The distinction between formal principal 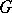 -objects and principal
-objects and principal 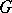 -objects is not a profound one: a necessary and sufficient condition for a formal principal
-objects is not a profound one: a necessary and sufficient condition for a formal principal 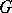 -object
-object 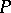 to be principal is that the unique morphism
to be principal is that the unique morphism 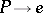 should form a covering of
should form a covering of  .
.
References
| [a1] | J. Giraud, "Cohomologie non abélienne" , Springer (1971) |
Principal G-object. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Principal_G-object&oldid=14516