Multi-sheeted region
From Encyclopedia of Mathematics
A region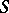 
of a Riemann surface 
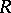, considered as a covering surface over the complex plane 
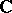, such that above each point of its projection 
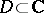there are at least two points of 
; a branch point of 
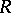of order 
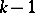is regarded here as 
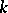distinct points. For example, the analytic function 
is a one-to-one mapping of the disc 
onto the two-sheeted region (two-sheeted disc) 
of the Riemann surface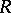 
of this function; this mapping is conformal everywhere except at the origin.
For analytic functions of several complex variables there arise multi-sheeted Riemann domains (cf. Riemannian domain) over the complex space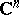 
.
Comments
References
| [a1] | C.L. Siegel, "Topics in complex functions" , 1 , Wiley (Interscience) (1988) pp. Chapt. 1, Sect. 4 |
| [a2] | G. Springer, "Introduction to Riemann surfaces" , Addison-Wesley (1957) pp. Chapt.10 |
How to Cite This Entry:
Multi-sheeted region. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Multi-sheeted_region&oldid=14503
Multi-sheeted region. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Multi-sheeted_region&oldid=14503
This article was adapted from an original article by E.D. Solomentsev (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article