Accessible random variable
A key concept in one of the mathematical models of the heuristic idea of white noise.
White noise should be a family  of independent identically distributed random variables. If the parameter set
of independent identically distributed random variables. If the parameter set  is the positive integers, there is no problem with this; indeed, sequences of independent identically distributed random variables appear repeatedly in probability and mathematical statistics. If
is the positive integers, there is no problem with this; indeed, sequences of independent identically distributed random variables appear repeatedly in probability and mathematical statistics. If  , it would seem natural to try the same thing, that is, to take
, it would seem natural to try the same thing, that is, to take  to be a family of independent identically distributed random variables. However, the independence means that
to be a family of independent identically distributed random variables. However, the independence means that 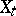 gives no information about
gives no information about 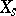 no matter how close
no matter how close  is to
is to  . This suggests that the process will be extremely irregular. Indeed, it can be shown that there is no measurable stochastic process of the type just described, see [a5]. Thus, one must look for other methods of modelling white noise in the case of a continuous parameter.
. This suggests that the process will be extremely irregular. Indeed, it can be shown that there is no measurable stochastic process of the type just described, see [a5]. Thus, one must look for other methods of modelling white noise in the case of a continuous parameter.
The best known method is instead to work with Brownian motion, regarding it as the integral of white noise. This is a beautiful, but highly technical, subject involving Itô stochastic integrals (cf. also Stochastic integral) and stochastic differential equations (cf. Stochastic differential equation) as well as the theory of continuous parameter semi-martingales (cf. Martingale), see [a3]. Another approach is to define white noise as the derivative of Brownian motion. Since Brownian paths are almost surely nowhere differentiable, the derivatives are interpreted in the distributional sense (cf. also Generalized function, derivative of a); see [a8].
The starting point of the approach to white noise involving accessible random variables is the closest to what is observed physically (at least in filtering problems in engineering).
Let  be a separable infinite-dimensional Hilbert space over
be a separable infinite-dimensional Hilbert space over 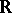 and let
and let 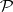 be the class of orthogonal projections on
be the class of orthogonal projections on 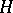 with finite-dimensional range. For
with finite-dimensional range. For  , let
, let
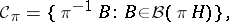 |
where 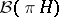 denotes the Borel subsets of
denotes the Borel subsets of 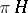 . Sets in
. Sets in 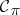 are called cylinder sets with base in
are called cylinder sets with base in 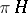 . Let
. Let  be the class of all cylinder sets in
be the class of all cylinder sets in 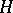 , that is,
, that is,
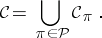 |
Each 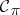 is a
is a 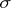 -field, but
-field, but 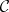 is only a field. The canonical Gaussian measure
is only a field. The canonical Gaussian measure 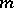 on
on  can be described as follows: Let
can be described as follows: Let 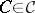 be given by
be given by 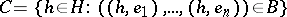 , where
, where 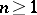 ,
, 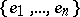 is an orthonormal set in
is an orthonormal set in 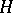 and
and 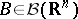 . Then
. Then
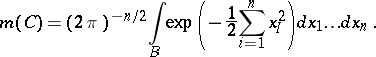 |
Note that the integrand above is the density function associated with  independent random variables, each distributed normally with mean
independent random variables, each distributed normally with mean  and variance
and variance 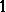 . Thus, the canonical Gauss measure is a straightforward infinite-dimensional analogue of the measure on
. Thus, the canonical Gauss measure is a straightforward infinite-dimensional analogue of the measure on  obtained by taking the product of
obtained by taking the product of  independent standard normal distributions on
independent standard normal distributions on  . In fact,
. In fact,  is not actually a measure, since it is only finitely additive on
is not actually a measure, since it is only finitely additive on 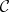 ; it is, however, countably additive (cf. Countably-additive set function) on each
; it is, however, countably additive (cf. Countably-additive set function) on each 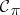 .
.
The "measure" 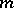 provides a simple and appealing starting point for an approach to Gaussian white noise, but the lack of countable additivity raises questions about the mathematical effectiveness of the model. This issue can be got around to a large extent by associating a true probability space
provides a simple and appealing starting point for an approach to Gaussian white noise, but the lack of countable additivity raises questions about the mathematical effectiveness of the model. This issue can be got around to a large extent by associating a true probability space 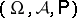 with the space
with the space  and making use of the countable additivity of
and making use of the countable additivity of 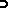 . It is in this context that "accessible random variables" arise.
. It is in this context that "accessible random variables" arise.
A representation of  is a pair
is a pair 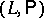 , where
, where  is a (countably additive) probability measure on a measurable space
is a (countably additive) probability measure on a measurable space 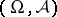 and
and  is a mapping (actually, an equivalence class of mappings, see [a6]) from
is a mapping (actually, an equivalence class of mappings, see [a6]) from 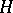 into a space of
into a space of 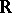 -valued random variables on
-valued random variables on  such that
such that 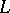 is linear, and such that, for all
is linear, and such that, for all 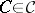 ,
,
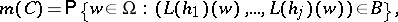 |
with 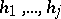 in
in  and
and 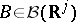 . The mapping
. The mapping 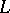 is linear in the sense that for any
is linear in the sense that for any 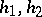 in
in 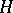 and
and  ,
, 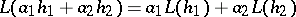
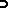 -almost surely. A representation of
-almost surely. A representation of  always exists, see [a6].
always exists, see [a6].
The following is an example of a representation: Take 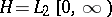 ,
, 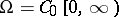 (the continuous functions on
(the continuous functions on 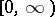 that vanish at
that vanish at  ),
), 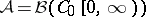 , and let
, and let  be Wiener measure on
be Wiener measure on 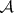 . Finally, given
. Finally, given 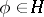 , let
, let 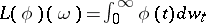 be the stochastic integral of
be the stochastic integral of 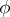 with respect to the Wiener path
with respect to the Wiener path 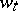 .
.
An accessible random variable will be defined in terms of Borel cylinder functions, a special class of accessible random variables. A function 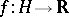 is called a Borel cylinder function if it can be written as
is called a Borel cylinder function if it can be written as 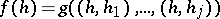 for some
for some 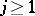 and
and 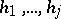 in
in 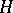 , where
, where 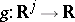 is Borel measurable. One defines
is Borel measurable. One defines 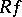 , the lifting of
, the lifting of 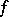 , by the formula
, by the formula
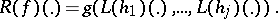 |
The space 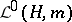 will consist of the functions
will consist of the functions 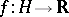 satisfying the condition: For all
satisfying the condition: For all  the function
the function 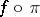 is
is 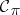 -measurable, and for all sequences
-measurable, and for all sequences 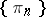 from
from 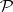 converging strongly to the identity, the sequence
converging strongly to the identity, the sequence 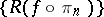 is Cauchy in
is Cauchy in  -probability. One can show that all such sequences converge in
-probability. One can show that all such sequences converge in  -probability to the same limit,
-probability to the same limit, 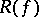 , called the lifting of
, called the lifting of  .
. 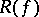 is defined
is defined  -almost surely. Any
-almost surely. Any 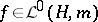 is called an accessible random variable.
is called an accessible random variable.
It is often desirable to put further restrictions on the function 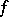 .
.  is defined as an analogue of the usual
is defined as an analogue of the usual 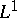 space. Given two representations and corresponding liftings, say
space. Given two representations and corresponding liftings, say 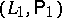 with
with 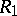 and
and 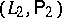 with
with 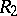 , and
, and 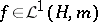 , one has
, one has
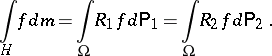 |
Thus, the integral of 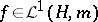 is independent of the representation and the lifting;
is independent of the representation and the lifting;  and
and 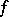 are the essential objects.
are the essential objects.
The situation just described is typical of much of the theory. The straightforward connection with observation is maintained through the role of 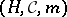 , but one also has the advantages of a countably additive probability space. It should be said, however, that the theory has its own technical difficulties and some frustrating open questions. For example, it is not always easy to tell whether a function is accessible or not, and it is unknown if
, but one also has the advantages of a countably additive probability space. It should be said, however, that the theory has its own technical difficulties and some frustrating open questions. For example, it is not always easy to tell whether a function is accessible or not, and it is unknown if 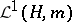 is complete (cf. Complete topological space).
is complete (cf. Complete topological space).
For a detailed discussion of white noise theory via the canonical Gaussian measure and accessible random variables, and for applications of that theory to non-linear filtering, see [a6]. It contains many references to the earlier literature, including references to the seminal work of I.E. Segal and L. Gross. Some more recent papers making use of the theory are [a1], [a4], [a7].
References
| [a1] | A. Budhiraja, G. Kallianpur, "Multiple Ogawa integrals, multiple Stratonovich integrals and the generalized Hu–Meyer formula" Techn. Report Dept. Stat. Univ. North Carolina , 442 (1994) |
| [a2] | T. Hida, H.H. Kuo, J. Potthoff, L. Streit, "White noise analysis" , World Sci. (1990) |
| [a3] | N. Ikeda, S. Watanabe, "Stochastic differential equations and diffusion processes" , North-Holland (1989) (Edition: Second) |
| [a4] | G.W. Johnson, G. Kallianpur, "Homogeneous chaos, 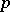 -forms, scaling and the Feynman integral" Trans. Amer. Math. Soc. , 340 (1993) pp. 503–548 -forms, scaling and the Feynman integral" Trans. Amer. Math. Soc. , 340 (1993) pp. 503–548 |
| [a5] | G. Kallianpur, "Stochastic filtering theory" , Springer (1980) |
| [a6] | G. Kallianpur, R.L. Karandikar, "White noise theory of prediction, filtering and smoothing" , Gordon&Breach (1988) |
| [a7] | G. Kallianpur, R.L. Karandikar, "Nonlinear transformations of the canonical Gauss measure on Hilbert space and absolute continuity" Acta Math. Appl. , 35 (1994) pp. 63–102 |
| [a8] | T. Hida, H.H. Kuo, J. Potthoff, L. Streit, "White noise. An infinite dimensional calculus" , Kluwer Acad. Publ. (1993) |
Accessible random variable. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Accessible_random_variable&oldid=14491