Permutation of a set
A one-to-one mapping of a set onto itself. The term permutation is used mainly for a finite set 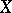 . In that case it is convenient to assume that
. In that case it is convenient to assume that 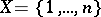 and to write the permutation in the form
and to write the permutation in the form
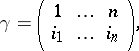 | (*) |
where 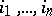 is a certain permutation of the numbers
is a certain permutation of the numbers 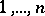 . The notation (*) means that
. The notation (*) means that  transforms the number
transforms the number 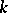 into
into 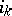 , i.e.
, i.e. 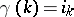 (one writes also
(one writes also  ) for
) for 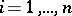 . The number of different permutations of a set
. The number of different permutations of a set 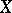 with
with  is equal to
is equal to 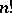 . The product of the permutations
. The product of the permutations 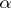 and
and 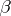 of a set
of a set 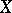 is defined as the successive application of the mappings
is defined as the successive application of the mappings 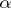 and
and 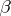 , and is given by the formula
, and is given by the formula 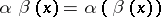 for all
for all 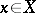 . The set of all permutations of
. The set of all permutations of 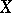 forms a group with respect to this multiplication, called the symmetric group. Any subgroup of a symmetric group is called a permutation group.
forms a group with respect to this multiplication, called the symmetric group. Any subgroup of a symmetric group is called a permutation group.
The symmetric group of permutations of a set 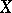 is denoted by
is denoted by 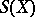 , and it contains as a subgroup
, and it contains as a subgroup 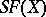 , the group consisting of those permutations
, the group consisting of those permutations 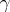 which displace only a finite subset of elements (i.e.
which displace only a finite subset of elements (i.e. 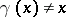 only for a finite set of elements
only for a finite set of elements 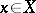 ). If
). If 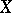 is finite and consists of
is finite and consists of  elements, the symmetric group is denoted by
elements, the symmetric group is denoted by 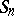 .
.
A transposition is a permutation of 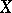 that displaces only two elements
that displaces only two elements  and
and 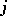 ; it is denoted by
; it is denoted by 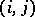 . In
. In 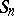 there are precisely
there are precisely  transpositions. Any permutation
transpositions. Any permutation 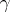 in
in 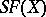 can be written as a product of transpositions. In particular, each permutation in
can be written as a product of transpositions. In particular, each permutation in 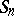 is a product of transpositions. A permutation can be written as a product of transpositions in many ways. However, for a given
is a product of transpositions. A permutation can be written as a product of transpositions in many ways. However, for a given 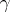 the parity of the number of factors in a decomposition of
the parity of the number of factors in a decomposition of 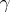 into transpositions is independent of the method of decomposing it. A permutation representable as a product of an even number of transpositions is called even, while one that decomposes as a product of an odd number of transpositions is called odd. In
into transpositions is independent of the method of decomposing it. A permutation representable as a product of an even number of transpositions is called even, while one that decomposes as a product of an odd number of transpositions is called odd. In 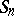 there are
there are 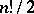 even permutations and the same number of odd ones. If a permutation
even permutations and the same number of odd ones. If a permutation 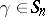 is written in the form (*), its parity coincides with the parity of the number of inversions in the permutation
is written in the form (*), its parity coincides with the parity of the number of inversions in the permutation 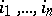 , i.e. it is equal to the number of pairs
, i.e. it is equal to the number of pairs 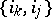 such that
such that 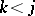 ,
, 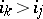 . A transposition is clearly an odd permutation. Composing a permutation with a single transposition alters the parity of the number of inversions. The product of two even permutations, and also of two odd ones, is an even permutation, while the product of an even and an odd permutation (in either order) is odd. The even permutations constitute a normal subgroup
. A transposition is clearly an odd permutation. Composing a permutation with a single transposition alters the parity of the number of inversions. The product of two even permutations, and also of two odd ones, is an even permutation, while the product of an even and an odd permutation (in either order) is odd. The even permutations constitute a normal subgroup 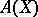 in the group
in the group 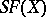 , called the alternating group. For
, called the alternating group. For  , the subgroup
, the subgroup 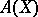 is denoted by
is denoted by 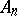 .
.
A cycle of length 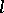 is a permutation
is a permutation  of a finite set
of a finite set 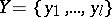 such that
such that
 |
A finite cycle is denoted by 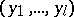 . An infinite cycle is a permutation of a countable set, of the form
. An infinite cycle is a permutation of a countable set, of the form
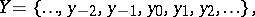 |
where for any integer 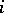 ,
, 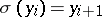 . The symbol for an infinite cycle is:
. The symbol for an infinite cycle is:
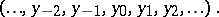 |
A cycle of length 2 is a transposition. The group 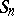 contains
contains 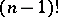 cycles of length
cycles of length  . For any permutation
. For any permutation 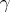 from
from 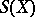 there exists a decomposition of
there exists a decomposition of 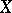 into non-intersecting subsets such that on each of them
into non-intersecting subsets such that on each of them 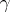 acts as a cycle. The finite subsets in this decomposition take the form
acts as a cycle. The finite subsets in this decomposition take the form
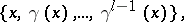 |
where 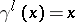 , while the infinite ones take the form
, while the infinite ones take the form
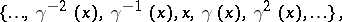 |
where 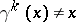 for
for 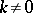 . The cycles induced by
. The cycles induced by 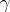 on the subsets of the decomposition are called disjoint cycles of the permutation
on the subsets of the decomposition are called disjoint cycles of the permutation 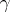 . For example,
. For example, 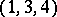 and
and 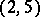 are disjoint cycles of the permutation
are disjoint cycles of the permutation
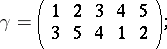 |
and 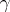 is written in the form
is written in the form
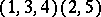 |
as the product of its disjoint cycles. In general, if 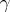 is not the identity permutation and has only a finite number of cycles of length greater than one, then
is not the identity permutation and has only a finite number of cycles of length greater than one, then 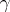 is the product of such cycles. In particular, each non-identity permutation from
is the product of such cycles. In particular, each non-identity permutation from 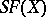 is the product of its disjoint cycles of length greater than one. The order of a permutation
is the product of its disjoint cycles of length greater than one. The order of a permutation 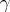 from
from 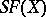 , i.e. the order of the cyclic group
, i.e. the order of the cyclic group 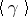 , is equal to the lowest common multiple of the lengths of its disjoint cycles.
, is equal to the lowest common multiple of the lengths of its disjoint cycles.
From the disjoint cycles of a given permutation one can obtain the disjoint cycles of any permutation conjugate with it (cf. Conjugate elements). For example, if
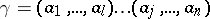 |
is the product of the disjoint cycles of the permutation 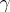 from
from 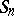 , if
, if 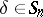 and if
and if 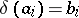 ,
, 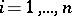 , then
, then
 |
is the decomposition of the permutation 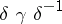 as a product of disjoint cycles. Two permutations of the group
as a product of disjoint cycles. Two permutations of the group 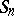 are conjugate in
are conjugate in 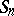 if and only if they have the same number of disjoint cycles of each length.
if and only if they have the same number of disjoint cycles of each length.
Let 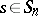 and let
and let 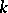 be the number of independent cycles of
be the number of independent cycles of  , including cycles of length 1. Then the difference
, including cycles of length 1. Then the difference 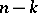 is called the decrement of the permutation
is called the decrement of the permutation  . The least number of factors in a decomposition of the permutation
. The least number of factors in a decomposition of the permutation  as a product of transpositions coincides with its decrement. The parity of a permutation coincides with the parity of its decrement.
as a product of transpositions coincides with its decrement. The parity of a permutation coincides with the parity of its decrement.
Permutations arose originally in combinatorics in the 18th century. At the end of the 18th century, J.L. Lagrange applied them in his research on the solvability of algebraic equations by radicals. A.L. Cauchy gave much attention to this topic, and was responsible, in particular, for the idea of expressing a permutation as a product of cycles. Research on the group properties of permutations has been carried out by N.H. Abel and, particularly, by E. Galois. See Galois theory and Permutation group.
References
| [1] | C. Jordan, "Traité des substitutions et des équations algébriques" , Paris (1957) |
| [2] | A.I. Kostrikin, "Introduction to algebra" , Springer (1982) (Translated from Russian) |
| [3] | A.G. Kurosh, "Higher algebra" , MIR (1972) (Translated from Russian) |
| [4] | M. Hall, "Group theory" , Macmillan (1959) |
Comments
In the notation 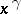 , the expression
, the expression 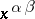 is to be read as
is to be read as 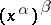 , i.e. first
, i.e. first 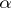 , then
, then 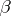 .
.
References
| [a1] | M. Suzuki, "Group theory" , 1–2 , Springer (1986) |
Permutation of a set. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Permutation_of_a_set&oldid=14475