Randomization
From Encyclopedia of Mathematics
A statistical procedure in which a decision is randomly taken. Suppose that, given a realization  of a random variable
of a random variable 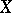 with values in a sample space
with values in a sample space 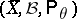 ,
, 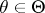 , one has to choose a solution
, one has to choose a solution  from a measurable space
from a measurable space 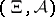 , and suppose that a family of so-called transition probability distributions
, and suppose that a family of so-called transition probability distributions 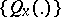 ,
,  , has been defined on
, has been defined on 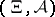 such that the function
such that the function 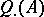 is
is 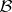 -measurable in
-measurable in  for every fixed event
for every fixed event 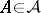 . Then randomization is the statistical procedure of decision taking in which, given a realization
. Then randomization is the statistical procedure of decision taking in which, given a realization  of
of 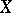 , the decision is made by drawing lots subject to the probability law
, the decision is made by drawing lots subject to the probability law 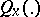 .
.
References
| [1] | N.N. [N.N. Chentsov] Čentsov, "Statistical decision rules and optimal inference" , Amer. Math. Soc. (1982) (Translated from Russian) |
Comments
The statistical procedure of randomization is also called a randomized decision rule.
References
| [a1] | J.O. Berger, "Statistical decision theory and Bayesian analysis" , Springer (1985) |
| [a2] | E.L. Lehmann, "Testing statistical hypotheses" , Wiley (1986) |
How to Cite This Entry:
Randomization. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Randomization&oldid=14463
Randomization. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Randomization&oldid=14463
This article was adapted from an original article by M.S. Nikulin (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article