Hilbert polynomial
of a graded module 
A polynomial expressing the dimensions of the homogeneous components of the module as a function of  for large natural numbers
for large natural numbers  . More exactly, the following theorem, demonstrated in essence by D. Hilbert, is valid. Let
. More exactly, the following theorem, demonstrated in essence by D. Hilbert, is valid. Let  be a ring of polynomials over a field
be a ring of polynomials over a field  , graded so that the
, graded so that the  are homogeneous elements of the first degree, and let
are homogeneous elements of the first degree, and let  be a graded
be a graded  -module of finite type; then there exists a polynomial
-module of finite type; then there exists a polynomial  with rational coefficients such that, for sufficiently large
with rational coefficients such that, for sufficiently large  ,
, 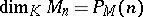 . This polynomial is called the Hilbert polynomial.
. This polynomial is called the Hilbert polynomial.
Of greatest interest is the interpretation of the Hilbert polynomial of a graded ring 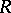 which is the quotient ring of the ring
which is the quotient ring of the ring 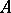 by a homogeneous ideal
by a homogeneous ideal 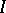 ; in such a case the Hilbert polynomial gives the projective invariants of the projective variety
; in such a case the Hilbert polynomial gives the projective invariants of the projective variety  defined by the ideal
defined by the ideal 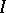 . In particular, the degree of
. In particular, the degree of  coincides with the dimension of
coincides with the dimension of 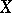 , while
, while 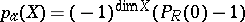 is said to be the arithmetic genus of
is said to be the arithmetic genus of 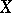 . Hilbert polynomials also serve to express the degree of the imbedding
. Hilbert polynomials also serve to express the degree of the imbedding 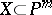 . The Hilbert polynomial of the ring
. The Hilbert polynomial of the ring 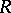 is also the name given to the Hilbert polynomial of the projective variety
is also the name given to the Hilbert polynomial of the projective variety 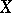 with respect to the imbedding
with respect to the imbedding  . If
. If  is the invertible sheaf corresponding to this imbedding, then
is the invertible sheaf corresponding to this imbedding, then
 |
for sufficiently large  .
.
References
| [1] | D. Hilbert, "Gesammelte Abhandlungen" , 2 , Springer (1933) |
| [2] | M. Baldassarri, "Algebraic varieties" , Springer (1956) |
| [3] | O. Zariski, P. Samuel, "Commutative algebra" , 1 , Springer (1975) |
Hilbert polynomial. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Hilbert_polynomial&oldid=14449