Functions on which K. Weierstrass based his general theory of elliptic functions (cf. Elliptic function), exposed in 1862 in his lectures at the University of Berlin [1], [2]. As distinct from the earlier structure of the theory of elliptic functions developed by A. Legendre, N.H. Abel and C.G. Jacobi, which was based on elliptic functions of the second order with two simple poles in the period parallelogram, a Weierstrass elliptic function has one second-order pole in the period parallelogram. From the theoretical point of view the theory of Weierstrass is simpler, since the function 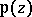 , on which it is based, and its derivative serve as elliptic functions which generate the algebraic field of elliptic functions with given primitive periods.
, on which it is based, and its derivative serve as elliptic functions which generate the algebraic field of elliptic functions with given primitive periods.
The Weierstrass 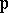 -function
-function 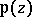 (
( is Weierstrass' notation) for given primitive periods
is Weierstrass' notation) for given primitive periods 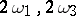 ,
,  , is defined as the series
, is defined as the series
 | (1) |
where 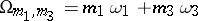 , and
, and 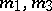 run through all integers except
run through all integers except 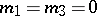 . The function
. The function 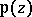 is an even elliptic function of order 2, with a unique second-order pole with zero residue in each period parallelogram. Its derivative
is an even elliptic function of order 2, with a unique second-order pole with zero residue in each period parallelogram. Its derivative 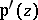 is an odd elliptic function of order 3 with the same primitive periods;
is an odd elliptic function of order 3 with the same primitive periods; 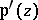 has simple zeros at points congruent with
has simple zeros at points congruent with 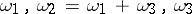 . The most important property of the function
. The most important property of the function 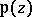 is that any elliptic function with given primitive periods
is that any elliptic function with given primitive periods 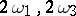 may be represented as a rational function of
may be represented as a rational function of  and
and 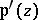 , i.e.
, i.e. 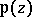 and
and 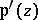 generate the algebraic field of elliptic functions with given periods. The simply-periodic trigonometric function which serves as the analogue of the function
generate the algebraic field of elliptic functions with given periods. The simply-periodic trigonometric function which serves as the analogue of the function  is
is 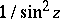 .
.
The function 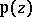 satisfies the differential equation
satisfies the differential equation
 | (2) |
in which the modular forms
are said to be the relative invariants and 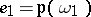 ,
, 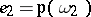 ,
, 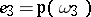 are said to be the irrational invariants of the function
are said to be the irrational invariants of the function 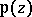 . An absolute invariant of
. An absolute invariant of 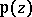 is any rational function of
is any rational function of 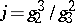 or of
or of 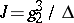 , where
, where 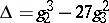 is the discriminant; this invariance is with respect to modular transformations (cf. Modular function). In applications,
is the discriminant; this invariance is with respect to modular transformations (cf. Modular function). In applications, 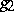 and
and 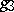 are usually real; if, in addition,
are usually real; if, in addition, 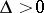 , then
, then 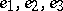 are also real. Equation (2) shows that
are also real. Equation (2) shows that 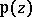 may be defined as the inverse of the elliptic integral of the first kind in Weierstrass normal form:
may be defined as the inverse of the elliptic integral of the first kind in Weierstrass normal form:
The function 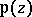 is a one-to-one conformal mapping of the period parallelogram onto a canonically cut two-sheet compact Riemann surface
is a one-to-one conformal mapping of the period parallelogram onto a canonically cut two-sheet compact Riemann surface 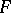 with branch points
with branch points  , of genus 1; the surface
, of genus 1; the surface 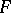 is sometimes said to be an elliptic image. The above integral of the first kind is single-valued on the principal covering surface
is sometimes said to be an elliptic image. The above integral of the first kind is single-valued on the principal covering surface 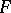 and is a uniformizing variable on
and is a uniformizing variable on 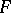 .
.
The elliptic integral of the second kind of the field of elliptic functions with given periods 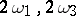 becomes, as a result of this uniformization, the Weierstrass zeta-function
becomes, as a result of this uniformization, the Weierstrass zeta-function 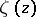 , which is defined by the series
, which is defined by the series
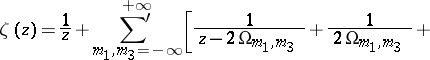 | (3) |
The function 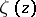 is an odd meromorphic function and is connected with
is an odd meromorphic function and is connected with 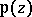 by the relation
by the relation 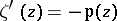 . It is not periodic, and if periods are added to its independent variable, it transforms according to
. It is not periodic, and if periods are added to its independent variable, it transforms according to  , where
, where 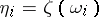 . The Legendre relation holds between
. The Legendre relation holds between 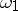 ,
, 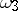 ,
, 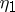 ,
, 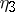 :
:
which is equivalent to a relation between complete elliptic integrals:
Any elliptic function 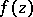 with given periods
with given periods 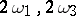 may be expressed in terms of
may be expressed in terms of 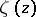 by the formula of Hermite:
by the formula of Hermite:
 | (4) |
where 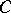 is a constant,
is a constant, 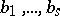 is the complete system of poles of
is the complete system of poles of 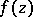 and the numbers
and the numbers 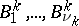 are the coefficients of the principal part of the Laurent expansion of
are the coefficients of the principal part of the Laurent expansion of 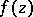 in a neighbourhood of
in a neighbourhood of 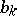 . The expansion (4) is the analogue of the expansion of an arbitrary rational function into partial fractions. The trigonometric function which is the analogue of the function
. The expansion (4) is the analogue of the expansion of an arbitrary rational function into partial fractions. The trigonometric function which is the analogue of the function 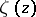 is
is 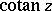 .
.
The Weierstrass sigma-function 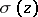 is defined as the infinite product
is defined as the infinite product
The function 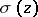 is an odd entire function with zeros
is an odd entire function with zeros 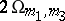 , and is connected with the functions
, and is connected with the functions 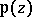 and
and 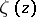 by the relations
by the relations
It is not a doubly-periodic function; the identities
where
apply.
An arbitrary elliptic function 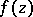 with periods
with periods 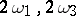 can be expressed in terms of
can be expressed in terms of  as:
as:
where 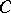 is a constant and
is a constant and  ,
, 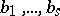 are the complete system of zeros and poles of
are the complete system of zeros and poles of 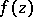 . The trigonometric function which is the analogue of the function
. The trigonometric function which is the analogue of the function 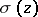 is
is 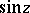 .
.
The following indexed sigma-functions are also important in Weierstrass' theory:
The functions 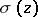 ,
, 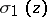 ,
, 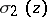 ,
, 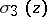 can be expressed in terms of the theta-functions (cf. Theta-function)
can be expressed in terms of the theta-functions (cf. Theta-function)  ,
, 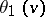 ,
, 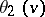 ,
, 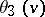 (cf. Jacobi elliptic functions), while the function
(cf. Jacobi elliptic functions), while the function 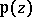 can be expressed in terms of
can be expressed in terms of  ,
, 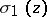 ,
, 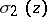 ,
, 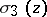 . The latter form the calculating base of Weierstrass' functions. It is also possible to obtain an explicit expression of the Weierstrass elliptic functions in terms of the Jacobi elliptic functions, e.g. in the form:
. The latter form the calculating base of Weierstrass' functions. It is also possible to obtain an explicit expression of the Weierstrass elliptic functions in terms of the Jacobi elliptic functions, e.g. in the form:
In applied problems the relative invariants 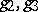 are usually given. The primitive periods
are usually given. The primitive periods 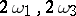 are usually computed with the aid of the absolute invariant
are usually computed with the aid of the absolute invariant 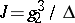 , which is a modular function of the ratio of the periods
, which is a modular function of the ratio of the periods 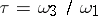 (see also Modular function).
(see also Modular function).
References
| [1] | K. Weierstrass, "Math. Werke" , 1–2 , Mayer & Müller (1894–1895) |
| [2] | H.A. Schwarz, "Formeln und Lehrsätze zum Gebrauche der elliptischen Funktionen" , Berlin (1893) |
| [3] | A. Hurwitz, R. Courant, "Vorlesungen über allgemeine Funktionentheorie und elliptische Funktionen" , 2 , Springer (1964) pp. Chapt.8 |
| [4] | E.T. Whittaker, G.N. Watson, "A course of modern analysis" , Cambridge Univ. Press (1952) pp. Chapt. 6 |
| [5] | N.I. Akhiezer, "Elements of the theory of elliptic functions" , Amer. Math. Soc. (1990) (Translated from Russian) |
References
| [a1] | J. Tannéry, J. Molk, "Eléments de la théorie des fonctions elliptiques" , 1–2 , Chelsea, reprint (1972) |
| [a2] | S. Lang, "Elliptic functions" , Addison-Wesley (1973) |
| [a3] | D.F. Lawden, "Elliptic functions and applications" , Springer (1989) |
| [a4] | A. Weil, "Elliptic functions according to Eisenstein and Kronecker" , Springer (1976) |
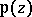 , on which it is based, and its derivative serve as elliptic functions which generate the algebraic field of elliptic functions with given primitive periods.
, on which it is based, and its derivative serve as elliptic functions which generate the algebraic field of elliptic functions with given primitive periods.
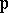 -function
-function 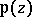 (
( is Weierstrass' notation) for given primitive periods
is Weierstrass' notation) for given primitive periods 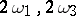 ,
,  , is defined as the series
, is defined as the series

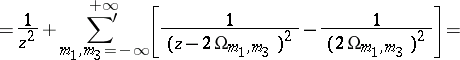
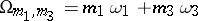 , and
, and 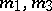 run through all integers except
run through all integers except 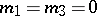 . The function
. The function 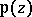 is an even elliptic function of order 2, with a unique second-order pole with zero residue in each period parallelogram. Its derivative
is an even elliptic function of order 2, with a unique second-order pole with zero residue in each period parallelogram. Its derivative 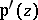 is an odd elliptic function of order 3 with the same primitive periods;
is an odd elliptic function of order 3 with the same primitive periods; 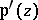 has simple zeros at points congruent with
has simple zeros at points congruent with 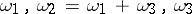 . The most important property of the function
. The most important property of the function 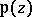 is that any elliptic function with given primitive periods
is that any elliptic function with given primitive periods 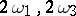 may be represented as a rational function of
may be represented as a rational function of  and
and 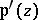 , i.e.
, i.e. 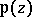 and
and 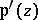 generate the algebraic field of elliptic functions with given periods. The simply-periodic trigonometric function which serves as the analogue of the function
generate the algebraic field of elliptic functions with given periods. The simply-periodic trigonometric function which serves as the analogue of the function  is
is 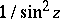 .
.
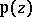 satisfies the differential equation
satisfies the differential equation

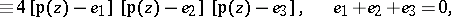
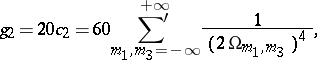
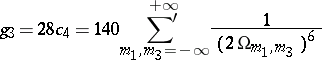
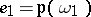 ,
, 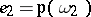 ,
, 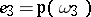 are said to be the irrational invariants of the function
are said to be the irrational invariants of the function 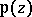 . An absolute invariant of
. An absolute invariant of 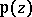 is any rational function of
is any rational function of 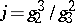 or of
or of 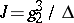 , where
, where 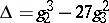 is the discriminant; this invariance is with respect to modular transformations (cf. Modular function). In applications,
is the discriminant; this invariance is with respect to modular transformations (cf. Modular function). In applications, 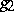 and
and 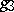 are usually real; if, in addition,
are usually real; if, in addition, 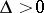 , then
, then 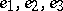 are also real. Equation (2) shows that
are also real. Equation (2) shows that 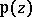 may be defined as the inverse of the elliptic integral of the first kind in Weierstrass normal form:
may be defined as the inverse of the elliptic integral of the first kind in Weierstrass normal form:
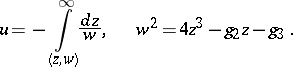
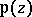 is a one-to-one conformal mapping of the period parallelogram onto a canonically cut two-sheet compact Riemann surface
is a one-to-one conformal mapping of the period parallelogram onto a canonically cut two-sheet compact Riemann surface 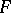 with branch points
with branch points  , of genus 1; the surface
, of genus 1; the surface 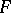 is sometimes said to be an elliptic image. The above integral of the first kind is single-valued on the principal covering surface
is sometimes said to be an elliptic image. The above integral of the first kind is single-valued on the principal covering surface 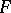 and is a uniformizing variable on
and is a uniformizing variable on 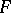 .
.
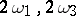 becomes, as a result of this uniformization, the Weierstrass zeta-function
becomes, as a result of this uniformization, the Weierstrass zeta-function 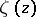 , which is defined by the series
, which is defined by the series
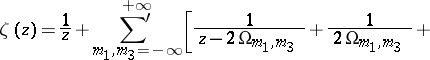

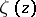 is an odd meromorphic function and is connected with
is an odd meromorphic function and is connected with 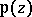 by the relation
by the relation 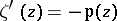 . It is not periodic, and if periods are added to its independent variable, it transforms according to
. It is not periodic, and if periods are added to its independent variable, it transforms according to  , where
, where 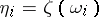 . The Legendre relation holds between
. The Legendre relation holds between 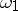 ,
, 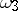 ,
, 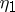 ,
, 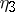 :
:
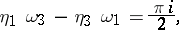
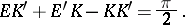
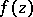 with given periods
with given periods 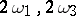 may be expressed in terms of
may be expressed in terms of 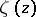 by the formula of Hermite:
by the formula of Hermite:

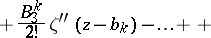
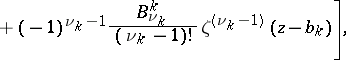
 is a constant,
is a constant, 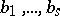 is the complete system of poles of
is the complete system of poles of  and the numbers
and the numbers 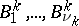 are the coefficients of the principal part of the Laurent expansion of
are the coefficients of the principal part of the Laurent expansion of 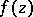 in a neighbourhood of
in a neighbourhood of 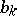 . The expansion (4) is the analogue of the expansion of an arbitrary rational function into partial fractions. The trigonometric function which is the analogue of the function
. The expansion (4) is the analogue of the expansion of an arbitrary rational function into partial fractions. The trigonometric function which is the analogue of the function 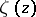 is
is 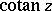 .
.
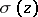 is defined as the infinite product
is defined as the infinite product
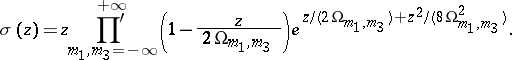
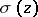 is an odd entire function with zeros
is an odd entire function with zeros 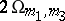 , and is connected with the functions
, and is connected with the functions 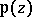 and
and 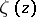 by the relations
by the relations
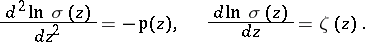
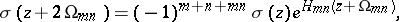
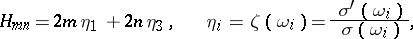
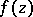 with periods
with periods 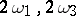 can be expressed in terms of
can be expressed in terms of  as:
as:
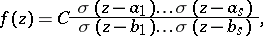
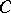 is a constant and
is a constant and  ,
, 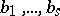 are the complete system of zeros and poles of
are the complete system of zeros and poles of 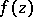 . The trigonometric function which is the analogue of the function
. The trigonometric function which is the analogue of the function 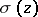 is
is 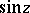 .
.
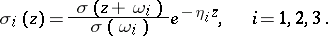
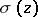 ,
, 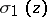 ,
, 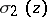 ,
, 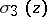 can be expressed in terms of the theta-functions (cf. Theta-function)
can be expressed in terms of the theta-functions (cf. Theta-function)  ,
, 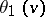 ,
, 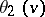 ,
, 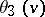 (cf. Jacobi elliptic functions), while the function
(cf. Jacobi elliptic functions), while the function 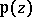 can be expressed in terms of
can be expressed in terms of  ,
, 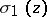 ,
, 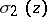 ,
, 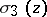 . The latter form the calculating base of Weierstrass' functions. It is also possible to obtain an explicit expression of the Weierstrass elliptic functions in terms of the Jacobi elliptic functions, e.g. in the form:
. The latter form the calculating base of Weierstrass' functions. It is also possible to obtain an explicit expression of the Weierstrass elliptic functions in terms of the Jacobi elliptic functions, e.g. in the form:
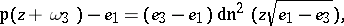
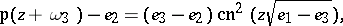
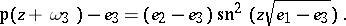
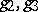 are usually given. The primitive periods
are usually given. The primitive periods 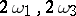 are usually computed with the aid of the absolute invariant
are usually computed with the aid of the absolute invariant 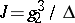 , which is a modular function of the ratio of the periods
, which is a modular function of the ratio of the periods 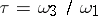 (see also Modular function).
(see also Modular function).