Ramification theory of valued fields
A branch of commutative algebra and number theory in which certain distinguished intermediate fields of algebraic extensions of fields equipped with a valuation are considered. Let 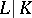 be a (not necessarily finite) algebraic extension of fields, and let
be a (not necessarily finite) algebraic extension of fields, and let 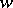 be a valuation of
be a valuation of  with valuation ring
with valuation ring 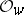 and extending a valuation
and extending a valuation  of
of 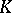 . Assume that the extension
. Assume that the extension 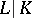 is normal (cf. Extension of a field) and that
is normal (cf. Extension of a field) and that 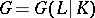 is its Galois group. The subgroup
is its Galois group. The subgroup
 |
of 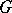 is called the decomposition group of
is called the decomposition group of  , and its fixed field
, and its fixed field  the decomposition field. The subgroup
the decomposition field. The subgroup
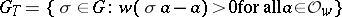 |
of 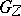 is called the inertia group, and its fixed field
is called the inertia group, and its fixed field 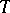 the inertia field. The subgroup
the inertia field. The subgroup
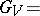 |
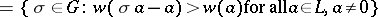 |
of 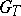 is called the ramification group, and its fixed field
is called the ramification group, and its fixed field 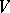 the ramification field. If
the ramification field. If 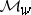 denotes the (unique) maximal ideal of
denotes the (unique) maximal ideal of 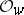 , then the condition
, then the condition 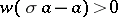 is equivalent to
is equivalent to 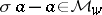 , and
, and 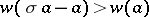 is equivalent to
is equivalent to
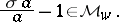 |
In number theory, also the higher ramification groups (cf. Ramified prime ideal) play a role; see [a2]. If the value group 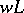 is a subgroup of the real numbers and
is a subgroup of the real numbers and  is a real number, then the
is a real number, then the  th ramification group is defined to be
th ramification group is defined to be
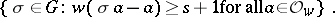 |
Basic properties.
Let 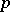 denote the characteristic of the residue field
denote the characteristic of the residue field  if it is a positive prime number; otherwise, set
if it is a positive prime number; otherwise, set  . For simplicity, denote the restriction of
. For simplicity, denote the restriction of 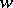 to the intermediate fields again by
to the intermediate fields again by 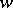 . Then
. Then 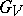 is a pro-
is a pro-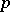 -group; in particular,
-group; in particular, 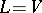 if the characteristic of
if the characteristic of 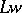 is
is  . The quotient group
. The quotient group 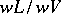 of the respective value groups is a
of the respective value groups is a 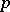 -group, and the extension
-group, and the extension 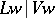 of the respective residue fields is purely inseparable (cf. Separable extension).
of the respective residue fields is purely inseparable (cf. Separable extension). 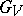 and
and 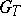 are normal subgroups of
are normal subgroups of  , and
, and 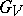 is a normal subgroup of
is a normal subgroup of 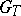 .
.
The Galois group  of the normal separable extension
of the normal separable extension  is isomorphic to the character group
is isomorphic to the character group 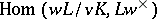 , which is (non-canonically) isomorphic to
, which is (non-canonically) isomorphic to  if this group is finite. One has
if this group is finite. One has 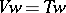 , and the group
, and the group  is
is 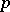 -prime, i.e., no element has an order divisible by
-prime, i.e., no element has an order divisible by 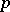 . Every finite quotient of the profinite group
. Every finite quotient of the profinite group 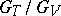 is
is 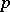 -prime.
-prime.
The Galois group 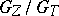 of the normal separable extension
of the normal separable extension 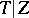 is isomorphic to the Galois group of the normal extensions
is isomorphic to the Galois group of the normal extensions 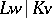 (which is
(which is 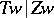 ). Furthermore,
). Furthermore, 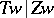 is separable, and
is separable, and  . The extension of
. The extension of  from
from 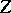 to
to 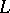 is unique. The extension
is unique. The extension  is purely inseparable, and
is purely inseparable, and 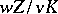 is a
is a 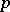 -group.
-group.
For many applications, it is more convenient to define the decomposition, inertia and ramification field to be the fixed field of the corresponding group in the maximal separable subextension of 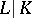 . Then one obtains the following additional properties:
. Then one obtains the following additional properties:  ;
; 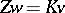 ;
; 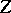 is the minimal subextension which admits a unique extension of
is the minimal subextension which admits a unique extension of 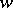 to
to 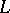 ;
; 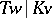 is the maximal separable subextension of
is the maximal separable subextension of 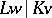 ; and
; and  is the maximal of all subgroups
is the maximal of all subgroups 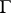 of
of 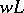 for which
for which 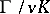 is
is  -prime.
-prime.
Absolute ramification theory.
Let 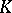 be any field with a valuation
be any field with a valuation  , and let
, and let 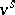 be some extension of
be some extension of  to the separable-algebraic closure
to the separable-algebraic closure 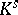 of
of  . Then the intermediate fields
. Then the intermediate fields  are called the absolute decomposition field, the absolute inertia field and the absolute ramification field, respectively. Since all extensions of
are called the absolute decomposition field, the absolute inertia field and the absolute ramification field, respectively. Since all extensions of  to
to 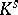 are conjugate, that is, of the form
are conjugate, that is, of the form 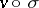 for
for  , it follows that these fields are independent of the choice of the extension
, it follows that these fields are independent of the choice of the extension  , up to isomorphism over
, up to isomorphism over 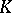 . The absolute ramification field is the Henselization of
. The absolute ramification field is the Henselization of 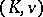 inside
inside 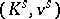 (see Henselization of a valued field); it coincides with
(see Henselization of a valued field); it coincides with  if and only if the extension of
if and only if the extension of  from
from  to every algebraic extension field is unique.
to every algebraic extension field is unique.
Tame extensions and defectless fields.
An extension  of
of  is called tamely ramified if
is called tamely ramified if 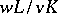 is
is 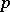 -prime and
-prime and 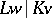 is separable. Let
is separable. Let 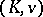 be Henselian. Then an extension of
be Henselian. Then an extension of 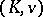 is called a tame extension if it is algebraic, tamely ramified and the defect of every finite subextension is trivial, that is, equal to
is called a tame extension if it is algebraic, tamely ramified and the defect of every finite subextension is trivial, that is, equal to 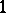 . The absolute ramification field is the unique maximal tame extension of
. The absolute ramification field is the unique maximal tame extension of  . If it is algebraically closed, or equivalently, if all algebraic extensions of
. If it is algebraically closed, or equivalently, if all algebraic extensions of 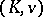 are tame extensions, then
are tame extensions, then 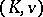 is called a tame field; see also Model theory of valued fields. From the fact that every finite subextension in the absolute ramification field is defectless it follows that a non-trivial defect can only appear between the absolute ramification field and the algebraic closure of
is called a tame field; see also Model theory of valued fields. From the fact that every finite subextension in the absolute ramification field is defectless it follows that a non-trivial defect can only appear between the absolute ramification field and the algebraic closure of 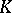 . Since every finite subextension of this extension has as degree a power of
. Since every finite subextension of this extension has as degree a power of 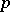 , the defect must be a power of
, the defect must be a power of  . This is the content of the Ostrowski lemma. In particular, the defect is always trivial if
. This is the content of the Ostrowski lemma. In particular, the defect is always trivial if  , that is, if the characteristic of
, that is, if the characteristic of 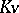 is
is  .
.
References
| [a1] | O. Endler, "Valuation theory" , Springer (1972) |
| [a2] | J.P. Serre, "Corps locaux" , Hermann (1962) |
Ramification theory of valued fields. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Ramification_theory_of_valued_fields&oldid=14401