Cell complex
A separable space 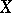 that is a union of non-intersecting cells. Here, by a
that is a union of non-intersecting cells. Here, by a  -dimensional cell one means a topological space that is homeomorphic to the interior of the unit cube of dimension
-dimensional cell one means a topological space that is homeomorphic to the interior of the unit cube of dimension  . If for each
. If for each  -dimensional cell
-dimensional cell 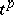 of
of  one is given a continuous mapping
one is given a continuous mapping  from the
from the 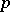 -dimensional cube
-dimensional cube  into
into 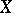 such that: 1) the restriction
such that: 1) the restriction 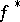 of
of  to the interior
to the interior 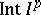 of
of 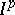 is one-to-one and the image
is one-to-one and the image  is the closure
is the closure 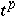 in
in 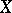 of
of 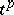 (here
(here 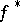 is a homeomorphism of
is a homeomorphism of  onto
onto  ); and 2) the set
); and 2) the set 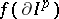 , where
, where 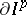 is the boundary of
is the boundary of  , is contained in the union
, is contained in the union 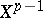 of the cells
of the cells 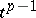 of
of 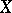 , then
, then 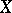 is called a cell complex; the union
is called a cell complex; the union 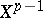 is called the skeleton of dimension
is called the skeleton of dimension  of the cell complex
of the cell complex 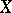 . An example of a cell complex is a simplicial polyhedron.
. An example of a cell complex is a simplicial polyhedron.
A subset 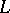 of a cell complex
of a cell complex 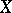 is called a subcomplex if it is a union of cells of
is called a subcomplex if it is a union of cells of 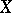 containing the closures of such cells. Thus, the
containing the closures of such cells. Thus, the  -dimensional skeleton
-dimensional skeleton  of
of 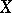 is a subcomplex of
is a subcomplex of  . Any union and any intersection of subcomplexes of
. Any union and any intersection of subcomplexes of 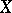 are subcomplexes of
are subcomplexes of  .
.
Any topological space can be regarded as a cell complex — as the union of its points, which are cells of dimension 0. This example shows that the notion of a cell complex is too broad; therefore narrower classes of cell complexes are important in applications, for example the class of cellular decompositions or CW-complexes (cf. CW-complex).
Cell complex. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Cell_complex&oldid=14376