Homogeneous space of an algebraic group
An algebraic variety  together with a regular transitive action of an algebraic group
together with a regular transitive action of an algebraic group  given on it. If
given on it. If 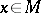 , then the isotropy group
, then the isotropy group  is closed in
is closed in  . Conversely, if
. Conversely, if  is a closed subgroup of an algebraic group
is a closed subgroup of an algebraic group  , then the set of left cosets
, then the set of left cosets  has the structure of an algebraic variety, making it into a homogeneous space of the algebraic group
has the structure of an algebraic variety, making it into a homogeneous space of the algebraic group  , where the natural mapping
, where the natural mapping 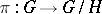 is regular, separable and has the following universal property: For any morphism
is regular, separable and has the following universal property: For any morphism 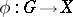 constant on cosets, there is a morphism
constant on cosets, there is a morphism 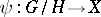 such that
such that 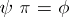 . If
. If  is any homogeneous space of the algebraic group
is any homogeneous space of the algebraic group 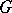 and
and  for some
for some 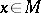 , then the natural bijection
, then the natural bijection 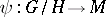 is regular, and if the ground field
is regular, and if the ground field 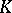 has characteristic 0, then
has characteristic 0, then  is biregular (see [1], [3]).
is biregular (see [1], [3]).
Suppose that the connected group 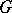 , the homogeneous space
, the homogeneous space  and the action of
and the action of 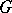 on
on 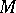 are defined over some subfield
are defined over some subfield 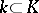 . Then the group of
. Then the group of 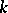 -rational points
-rational points 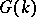 takes
takes  into itself and
into itself and 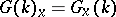 for
for 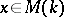 . If
. If 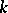 is finite, then
is finite, then 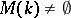 , and if moreover the isotropy group
, and if moreover the isotropy group 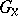 is connected, then
is connected, then 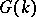 acts transitively on
acts transitively on 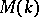 . In the general case, the study of the
. In the general case, the study of the 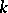 -rational points in
-rational points in 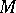 reduces to problems in the theory of Galois cohomology (see [2]).
reduces to problems in the theory of Galois cohomology (see [2]).
A homogeneous space of an algebraic group 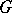 is always a smooth quasi-projective variety (see [5]). If
is always a smooth quasi-projective variety (see [5]). If 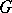 is an affine algebraic group, then the variety
is an affine algebraic group, then the variety  is projective if and only if
is projective if and only if 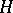 is a parabolic subgroup in
is a parabolic subgroup in 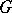 (see [3]). If
(see [3]). If  is reductive, then the variety
is reductive, then the variety 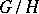 is affine if and only if the subgroup
is affine if and only if the subgroup  is reductive (see Matsushima criterion). A description is also known of the closed subgroups
is reductive (see Matsushima criterion). A description is also known of the closed subgroups  of a linear algebraic group
of a linear algebraic group 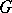 over an algebraically closed field of characteristic 0 for which
over an algebraically closed field of characteristic 0 for which 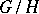 is quasi-affine (see [4], [6]).
is quasi-affine (see [4], [6]).
References
| [1] | A. Borel, "Linear algebraic groups" , Benjamin (1969) |
| [2] | J.-P. Serre, "Cohomologie Galoisienne" , Springer (1964) |
| [3] | J.E. Humphreys, "Linear algebraic groups" , Springer (1975) |
| [4] | A.A. Sukhanov, "A description of observable subgroups of linear algebraic groups" Math. USSR-Sb. , 68 (Forthcoming) Mat. Sb. , 137 : 1 (1988) pp. 90–102 |
| [5] | W. Chow, "On the projective embedding of homogeneous varieties" , Algebraic topology; symposium in honour of S. Lefschetz , Princeton Univ. Press (1957) pp. 122–128 |
| [6] | G.P. Hochschild, "Basic theory of algebraic groups and Lie algebras" , Springer (1981) |
Homogeneous space of an algebraic group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Homogeneous_space_of_an_algebraic_group&oldid=14365