Dirichlet L-function

Dirichlet 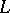-series, 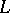-series

A function of a complex variable 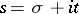that is defined for any Dirichlet character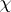 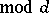by the series

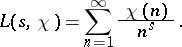(1)

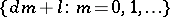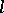As functions of a real variable these were introduced by P.G.L. Dirichlet [1] in 1837 in the context of the proof that the number of primes in an arithmetic progression , where the difference and the first term are relatively prime numbers, is infinite. They are a natural generalization of the Riemann zeta-function 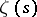to an arithmetic progression and are a powerful tool in analytic number theory [2]–[4].

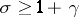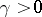The series (1), known as a Dirichlet series, converges absolutely and uniformly in any bounded domain in the complex -plane for which , . If 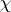is a non-principal character, one has

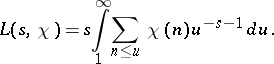(2)

Since the sum in the integrand is bounded, this formula gives an analytic continuation of 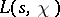to a regular function in the half-plane .

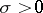For any 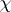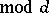it is possible to represent 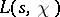as an Euler product over prime numbers :

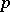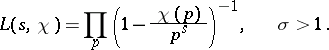(3)

Hence, if 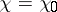is a principal character 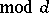, one has, for ,

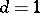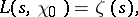and for ,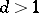

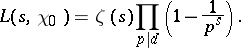For this reason the properties of 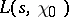in the entire complex plane are mainly determined by the properties of 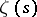. In particular, the function 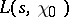is regular for all , except for 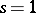where it has a simple pole with residue 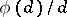; here 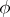is Euler's function. If, on the other hand, 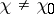and if 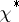is the primitive character inducing the character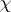 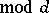, then

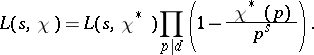(4)

Thus, it is no essential restriction to consider only Dirichlet 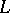-functions for primitive characters. This property of Dirichlet 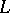-functions is important, since many results concerning 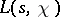have a simple form for primitive characters only. If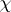 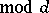is primitive, the analytic continuation to the entire plane and the functional equation for the function 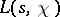are obtained by direct generalization of Riemann's method for 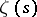. Putting

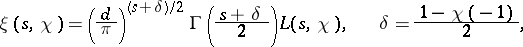the result has the form

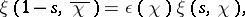(5)

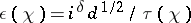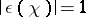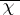where is the gamma-function, , , is a Gauss sum, and is the complex conjugate character to 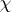. This equation is known as the functional equation of the function 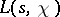. It follows from this formula and from formulas (2) and (4) that the functions 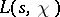and 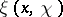are entire functions for all 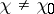; if 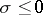, 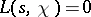only at the points 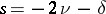, 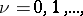and at the points where the product in (4) vanishes; these points are known as the trivial zeros of 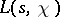. The remaining zeros of 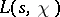are said to be the non-trivial zeros. If 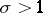, then 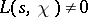. Ch.J. de la Vallée-Poussin showed that 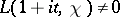, so that all non-trivial zeros of a Dirichlet 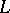-function lie in the domain 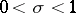, which is known as the critical strip.

The distribution of the non-trivial zeros, and of the values of 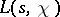in the critical strip in general, is the most important problem in the theory of Dirichlet 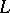-functions, and is of fundamental importance in number theory.

That each function 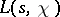has infinitely many non-trivial zeros, and that the laws governing the distribution of primes in arithmetic progressions directly depend on the distribution of these zeros, is shown by the corresponding analogues of Riemann's formulas. In fact, let 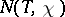be the number of zeros of the function 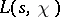with a primitive character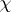 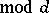in the rectangle 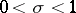, , 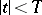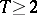. Then

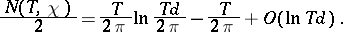Let 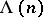be the Mangoldt function, 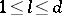, , 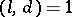and let

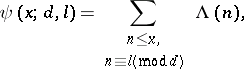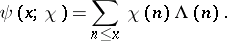Then it follows from the orthogonality property of the characters that

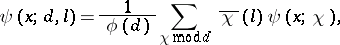(6)

where the summation is extended over all characters 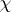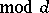. Moreover, for a primitive character and for :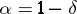

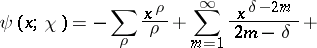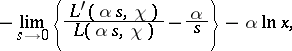where runs through the non-trivial zeros of 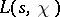, and 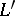is the derivative of 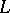with respect to .

Approximate formulas for 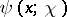are more useful in practice: For arbitrary 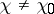and for 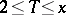one has

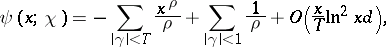(7)

and for ,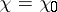

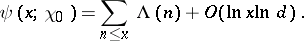(8)

The quantity in (8) is the principal term of the sum in (6).

According to the so-called extended Riemann hypothesis, all non-trivial zeros of a Dirichlet -function lie on the straight line 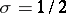. If this hypothesis is valid, one has, for ,

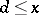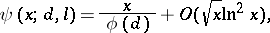and many other important problems in number theory would have their final solution. However, problems concerning the distribution of the non-trivial zeros of a Dirichlet 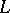-function are exceptionally difficult, and relatively little is yet (1988) known on the subject. Stronger results were obtained for complex rather than for real characters.

A generalization of the method proposed in 1899 by de la Vallée-Poussin for the function 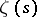yields a bound on the non-trivial zeros of 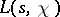: For a complex character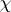 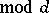there exists an absolute constant 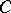such that 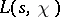has no zeros in the domain

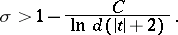However, if 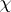is a real non-principal character modulo 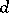, then 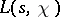may have in this domain at most one simple real (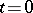) zero, known as the exceptional zero of 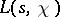. The following inequality was deduced for the exceptional zero 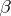from the analytic class number formula for quadratic fields:

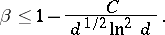A well-known best (pre 1975) bound for 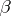was obtained in 1935 by C.L. Siegel: For any 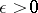there exists a positive number 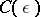such that

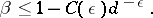However, this estimate has the major drawback of being ineffective in the sense that the knowledge of is insufficient to make an estimate for the numerical constant 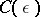. This is also the disadvantage of the number-theoretic results based on Siegel's estimate.

From the above bounds for the non-trivial zeros of Dirichlet 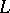-functions and formulas (6)–(8), the following asymptotic law for the distribution of prime numbers can be derived:

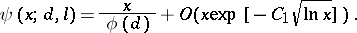Here 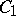is an effectively computable constant for 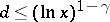for some 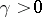. Otherwise, one has 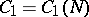ineffectively, where 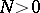is such that .

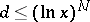These results are the best results available in the problem of uniform distribution of prime numbers in arithmetic progressions with increasing difference 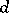. A little more is known in the case where the value of 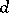is fixed. In such a case the theory of Dirichlet 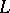-functions for 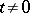resembles in many respects the theory of the Riemann zeta-function [5], and the most recent bound on the zeros of 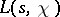, obtained by the Vinogradov method for estimating trigonometric sums, has the form:

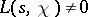for

where 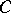is a positive constant depending on .

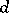To this bound for the non-trivial zeros of Dirichlet 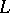-functions modulo a fixed 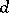corresponds the best (1977) remainder term in the asymptotic formula for :

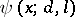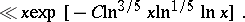All formulas concerning the asymptotics of the function 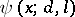have analogues for the function 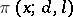, viz. for the number of primes 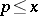, 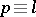(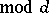), with principal term 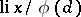instead of 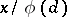and a residual term which is smaller by a factor .

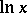A major subject in modern studies on the theory of Dirichlet 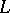-functions is research on the density of the distribution of the non-trivial zeros of such functions. This research is concerned with giving estimates for the quantities

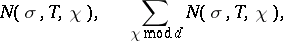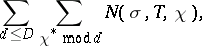where 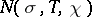denotes the number of zeros of 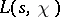in the rectangle 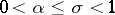, , 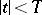and 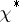is a primitive character .

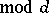References

[1]	P.G.L. Dirichlet, "Vorlesungen über Zahlentheorie" , Vieweg (1894)
[2]	H. Davenport, "Multiplicative number theory" , Springer (1980)
[3]	K. Prachar, "Primzahlverteilung" , Springer (1957)
[4]	N.G. Chudakov, "Introductions to the theory of Dirichlet -functions" , Moscow-Leningrad (1947) (In Russian)
[5]	A. Walfisz, "Weylsche Exponentialsummen in der neueren Zahlentheorie" , Deutsch. Verlag Wissenschaft. (1963)
[6]	H. Montgomery, "Topics in multiplicative number theory" , Springer (1971)
[7]	A.F. Lavrik, "Development of the method of density of zeros of Dirichlet -functions" Math. Notes , 17 : 5 (1975) pp. 483–488 Mat. Zametki , 17 : 5 (1975) pp. 809–817

Comments

The effective bound

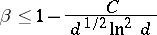for the exceptional zero 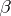of 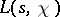, where 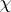is a real non-principal character 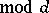, was improved by D. Goldfeld and A. Schinzel [a1] to

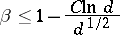for 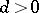and

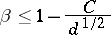for 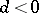. Here 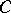is an effectively computable constant. Using work of B.H. Gross and D. Zagier [a2] the result for 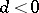can be improved to

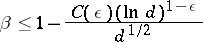for any 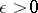, where 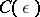is an effective constant.

References

[a1]	D. Goldfeld, A. Schinzel, "On Siegel's zero" Ann. Scuola Norm. Sup. Pisa Cl. Sci. (4) , 2 (1975) pp. 571–583
[a2]	B.H. Gross, D. Zagier, "Heegner points and derivatives of -series" Invent. Math. , 84 (1986) pp. 225–320