Covariant vector
An element of the vector space 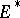 dual to an
dual to an  -dimensional vector space
-dimensional vector space 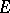 , that is, a linear functional (linear form) on
, that is, a linear functional (linear form) on 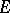 . In the ordered pair
. In the ordered pair 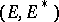 , an element of
, an element of 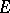 is called a contravariant vector. Within the general scheme for the construction of tensors, a covariant vector is identified with a covariant tensor of valency 1.
is called a contravariant vector. Within the general scheme for the construction of tensors, a covariant vector is identified with a covariant tensor of valency 1.
The coordinate notation for a covariant vector is particularly simple if one chooses in 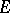 and
and 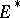 so-called dual bases
so-called dual bases  in
in 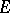 and
and 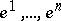 in
in 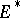 , that is, bases such that
, that is, bases such that 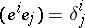 (where
(where 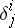 is the Kronecker symbol); an arbitrary covariant vector
is the Kronecker symbol); an arbitrary covariant vector 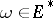 is then expressible in the form
is then expressible in the form 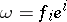 (summation over
(summation over 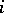 from 1 to
from 1 to  ), where
), where 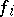 is the value of the linear form
is the value of the linear form 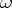 at the vector
at the vector 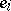 . On passing from dual bases
. On passing from dual bases 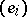 and
and 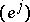 to dual bases
to dual bases 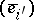 and
and 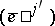 according to the formulas
according to the formulas
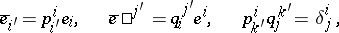 |
the coordinates 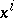 of the contravariant vector
of the contravariant vector 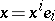 change according to the contravariant law
change according to the contravariant law 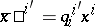 , while the coordinates
, while the coordinates 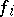 of the covariant vector
of the covariant vector 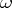 change according to the covariant law
change according to the covariant law 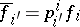 (i.e. they change in the same way as the basis, whence the terminology "covariant vectorcovariant" ).
(i.e. they change in the same way as the basis, whence the terminology "covariant vectorcovariant" ).
References
| [1] | P.A. Shirokov, "Tensor calculus. Tensor algebra" , Kazan' (1961) (In Russian) |
| [2] | D.V. Beklemishev, "A course of analytical geometry and linear algebra" , Moscow (1971) (In Russian) |
| [3] | J.A. Schouten, "Tensor analysis for physicists" , Cambridge Univ. Press (1951) |
Comments
References
| [a1] | M. Spivak, "A comprehensive introduction to differential geometry" , 1979 , Publish or Perish (1970–1975) pp. 1–5 |
Covariant vector. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Covariant_vector&oldid=14326