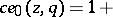The 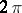 -periodic solutions of the Mathieu equation
-periodic solutions of the Mathieu equation
which exist only when the point 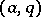 in the parameter plane lies on the boundary of the stability zones. A Mathieu function is even or odd, and is unique up to a factor; the second linearly-independent solution grows linearly in
in the parameter plane lies on the boundary of the stability zones. A Mathieu function is even or odd, and is unique up to a factor; the second linearly-independent solution grows linearly in  for
for 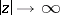 , provided
, provided 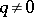 . The even Mathieu functions are the eigen functions of the integral equation
. The even Mathieu functions are the eigen functions of the integral equation
An analogous equation is satisfied by the odd Mathieu functions. The notation for Mathieu functions is:
For 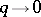 these functions reduce to the trigonometric system
these functions reduce to the trigonometric system
and they possess the same orthogonality properties on the interval 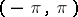 . The Mathieu functions admit Fourier-series expansions which converge for small
. The Mathieu functions admit Fourier-series expansions which converge for small 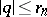 ; the coefficients of these series are convergent power series in
; the coefficients of these series are convergent power series in 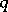 , for example,
, for example,
References
| [1] | E.T. Whittaker, G.N. Watson, "A course of modern analysis" , Cambridge Univ. Press (1952) pp. Chapt. 2 |
| [2] | H. Bateman (ed.) A. Erdélyi (ed.) , Higher transcendental functions , 3. Automorphic functions , McGraw-Hill (1955) |
| [3] | G. Sansone, "Equazioni differenziali nel campo reale" , 1 , Zanichelli (1948) |
| [4] | M.J.O. Strett, "Lamésche-, Mathieusche- und verwandte Funktionen in Physik und Technik" , Springer (1932) |
| [5] | N.W. Mac-Lachlan, "Theory and application of Mathieu functions" , Clarendon Press (1947) |
How to Cite This Entry:
Mathieu functions. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Mathieu_functions&oldid=14316
This article was adapted from an original article by M.V. Fedoryuk (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098.
See original article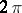 -periodic solutions of the Mathieu equation
-periodic solutions of the Mathieu equation
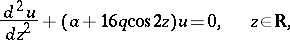
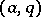 in the parameter plane lies on the boundary of the stability zones. A Mathieu function is even or odd, and is unique up to a factor; the second linearly-independent solution grows linearly in
in the parameter plane lies on the boundary of the stability zones. A Mathieu function is even or odd, and is unique up to a factor; the second linearly-independent solution grows linearly in  for
for 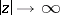 , provided
, provided 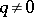 . The even Mathieu functions are the eigen functions of the integral equation
. The even Mathieu functions are the eigen functions of the integral equation
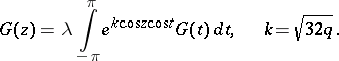

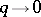 these functions reduce to the trigonometric system
these functions reduce to the trigonometric system

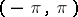 . The Mathieu functions admit Fourier-series expansions which converge for small
. The Mathieu functions admit Fourier-series expansions which converge for small 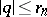 ; the coefficients of these series are convergent power series in
; the coefficients of these series are convergent power series in 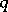 , for example,
, for example,