Linear functional
linear form, on a vector space  over a field
over a field 
A mapping  such that
such that
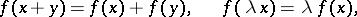 |
for all  ,
,  . The concept of a linear functional, as an important special case of the concept of a linear operator, is one of the main concepts in linear algebra and plays a significant role in analysis.
. The concept of a linear functional, as an important special case of the concept of a linear operator, is one of the main concepts in linear algebra and plays a significant role in analysis.
On the set  of linear functionals on
of linear functionals on  the operations of addition and multiplication by a scalar are defined according to the formulas
the operations of addition and multiplication by a scalar are defined according to the formulas
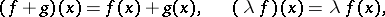 |
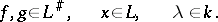 |
They specify in  a vector space structure over
a vector space structure over  .
.
The kernel of a linear functional is the subspace 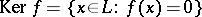 . If
. If 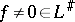 (that is,
(that is, 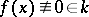 ), then
), then  is a hyperplane in
is a hyperplane in 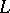 . Linear functionals with the same kernel are proportional.
. Linear functionals with the same kernel are proportional.
If 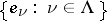 is a basis of
is a basis of 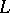 , then for
, then for
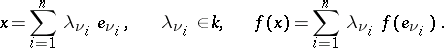 |
The correspondence 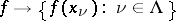 is an isomorphism of
is an isomorphism of  onto
onto 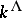 . Corollary:
. Corollary:  is isomorphic to
is isomorphic to  if and only if it is finite dimensional. On transition to a new basis in
if and only if it is finite dimensional. On transition to a new basis in 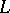 the elements
the elements 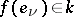 are transformed by the same formulas as the basis vectors.
are transformed by the same formulas as the basis vectors.
The operator 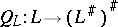 defined by
defined by 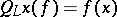 is injective. It is an isomorphism if and only if
is injective. It is an isomorphism if and only if 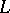 is finite dimensional. This isomorphism, in contrast to the isomorphism between
is finite dimensional. This isomorphism, in contrast to the isomorphism between 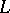 and
and  , is natural, i.e. functorial (cf. Functorial morphism).
, is natural, i.e. functorial (cf. Functorial morphism).
A linear functional on a locally convex space, in particular on a normed space, is an important object of study in functional analysis. Every continuous (as a mapping on topological spaces) linear functional 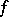 on a locally convex space
on a locally convex space  is bounded (cf. Bounded operator), that is,
is bounded (cf. Bounded operator), that is,
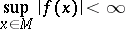 |
for all bounded 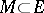 . If
. If  is a normed space, the converse is also true; both properties are then equivalent to the finiteness of the number
is a normed space, the converse is also true; both properties are then equivalent to the finiteness of the number
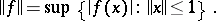 |
The continuous linear functionals on a locally convex space  form a subspace
form a subspace 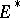 of
of  , which is said to be the dual of
, which is said to be the dual of 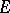 . In
. In 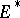 one considers different topologies, including the weak and strong topologies, which correspond, respectively, to pointwise and uniform convergence on bounded sets. If
one considers different topologies, including the weak and strong topologies, which correspond, respectively, to pointwise and uniform convergence on bounded sets. If  is a normed space, then
is a normed space, then 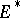 is a Banach space with respect to the norm
is a Banach space with respect to the norm 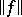 and the corresponding topology coincides with the strong topology. The unit ball
and the corresponding topology coincides with the strong topology. The unit ball 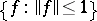 , considered in the weak topology, is compact.
, considered in the weak topology, is compact.
The Hahn–Banach theorem has important applications in analysis; one formulation of it is as follows: If  is a pre-norm on a vector space
is a pre-norm on a vector space 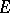 and if
and if  is a linear functional defined on a subspace
is a linear functional defined on a subspace 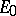 of
of 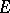 such that
such that 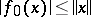 for all
for all 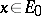 , then
, then 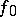 can be extended to the whole of
can be extended to the whole of  , preserving linearity and the given bound. Corollary: Any continuous linear functional defined on a subspace
, preserving linearity and the given bound. Corollary: Any continuous linear functional defined on a subspace 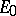 of a locally convex space
of a locally convex space 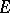 can be extended to a continuous linear functional on
can be extended to a continuous linear functional on 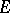 , and if
, and if  is a normed space, then the norm is preserved. Hence, for every
is a normed space, then the norm is preserved. Hence, for every 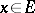 ,
, 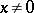 , there is an
, there is an  with
with  .
.
Let  be a normed space and suppose that
be a normed space and suppose that 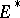 , and then
, and then 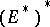 , are taken with the corresponding norms. Then the operator
, are taken with the corresponding norms. Then the operator
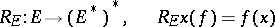 |
is an isometric imbedding. If under this imbedding  coincides with
coincides with  , then
, then  , which is necessarily complete, is said to be reflexive (cf. Reflexive space). For example,
, which is necessarily complete, is said to be reflexive (cf. Reflexive space). For example,  and
and  ,
, 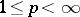 , are reflexive if and only if
, are reflexive if and only if  . There is a similar concept of reflexivity for general locally convex spaces.
. There is a similar concept of reflexivity for general locally convex spaces.
For many locally convex spaces, all linear functionals have been described. For example, the adjoint of a Hilbert space  is
is  . The adjoint of
. The adjoint of 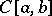 is
is  .
.
References
| [1] | N. Bourbaki, "Elements of mathematics. Algebra: Modules. Rings. Forms" , 2 , Addison-Wesley (1975) pp. Chapt.4;5;6 (Translated from French) |
| [2] | A.N. Kolmogorov, S.V. Fomin, "Elements of the theory of functions and functional analysis" , 1–2 , Graylock (1957–1961) (Translated from Russian) |
Comments
References
| [a1] | A.E. Taylor, D.C. Lay, "Introduction to functional analysis" , Wiley (1980) |
Linear functional. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Linear_functional&oldid=14314