Borel summation method
A method for summing series of functions, proposed by E. Borel [1]. Suppose one is given a series of numbers
 | (*) |
let 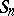 be its partial sums and let
be its partial sums and let 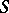 be a real number. The series (*) is summable by the Borel method (
be a real number. The series (*) is summable by the Borel method (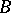 -method) to the number
-method) to the number 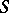 if
if
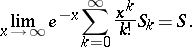 |
There exists an integral summation method due to Borel. This is the 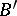 -method: If
-method: If
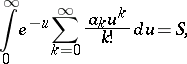 |
then one says that the series (*) is summable by the 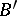 -method to the number
-method to the number 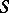 . For conditions under which the two methods
. For conditions under which the two methods 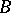 and
and 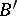 are equivalent, cf. [2]. The
are equivalent, cf. [2]. The  -method originated in the context of analytic extension of a function regular at a point. Let
-method originated in the context of analytic extension of a function regular at a point. Let
 |
be regular at the point 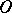 and let
and let 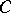 be the set of all its singular points. Draw the segment
be the set of all its singular points. Draw the segment  and the straight line
and the straight line  normal to
normal to  through any point
through any point  . The set of points on the same side with
. The set of points on the same side with 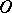 for each straight line
for each straight line 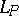 is denoted by
is denoted by 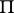 ; the boundary
; the boundary 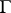 of the domain
of the domain 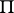 is then called the Borel polygon of the function
is then called the Borel polygon of the function 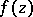 , while the domain
, while the domain 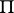 is called its interior domain. The following theorem is valid: The series
is called its interior domain. The following theorem is valid: The series
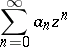 |
is summable by the 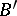 -method in
-method in 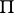 , but not in the domain
, but not in the domain 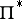 which is the complement of
which is the complement of 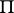 [2].
[2].
References
| [1] | E. Borel, "Mémoire sur les séries divergentes" Ann. Sci. École Norm. Sup. (3) , 16 (1899) pp. 9–131 |
| [2] | G.H. Hardy, "Divergent series" , Clarendon Press (1949) |
Comments
References
| [a1] | W. Beekmann, K. Zeller, "Theorie der Limitierungsverfahren" , Springer (1970) |
Borel summation method. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Borel_summation_method&oldid=14305