Poisson transform
From Encyclopedia of Mathematics
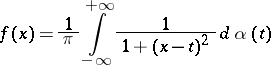 | (*) |
where  is a function of bounded variation in every finite interval, and also the transform
is a function of bounded variation in every finite interval, and also the transform
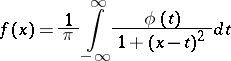 |
which results from (*) if  is an absolutely-continuous function (cf. Absolute continuity). Let
is an absolutely-continuous function (cf. Absolute continuity). Let
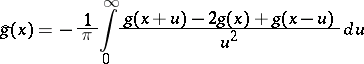 |
and let
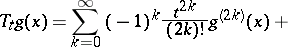 |
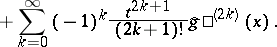 |
The following inversion formulas hold for the Poisson transform:
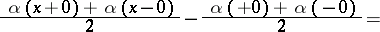 |
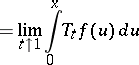 |
for all  , and
, and
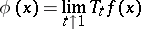 |
almost everywhere.
Let 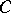 be a convex open acute cone in
be a convex open acute cone in 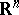 with vertex at zero and let
with vertex at zero and let 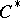 be the dual cone, that is,
be the dual cone, that is,
 |
The function
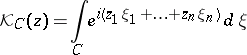 |
is called the Cauchy kernel of the tube domain 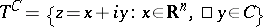 . The Poisson transform of a (generalized) function
. The Poisson transform of a (generalized) function 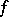 is the convolution (cf. Convolution of functions)
is the convolution (cf. Convolution of functions)
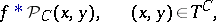 |
where
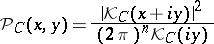 |
is the Poisson kernel of the tube domain 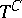 (see [2]).
(see [2]).
References
| [1] | H. Pollard, "The Poisson transform" Trans. Amer. Math. Soc. , 78 : 2 (1955) pp. 541–550 |
| [2] | V.S. Vladimirov, "Generalized functions in mathematical physics" , MIR (1977) (Translated from Russian) |
How to Cite This Entry:
Poisson transform. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Poisson_transform&oldid=14304
Poisson transform. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Poisson_transform&oldid=14304
This article was adapted from an original article by Yu.A. BrychkovA.P. Prudnikov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article