Number field
A field consisting of complex (e.g., real) numbers. A set of complex numbers forms a number field if and only if it contains more than one element and with any two elements 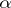 and
and 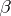 their difference
their difference 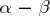 and quotient
and quotient 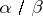 (
( ). Every number field contains infinitely many elements. The field of rational numbers is contained in every number field.
). Every number field contains infinitely many elements. The field of rational numbers is contained in every number field.
Examples of number fields are the fields of rational numbers, real numbers, complex numbers, or Gaussian numbers (cf. Gauss number). The set of all numbers of the form 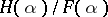 ,
, 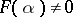 , forms a number field,
, forms a number field, 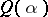 , where
, where 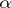 is a fixed complex number and
is a fixed complex number and  and
and 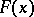 range over the polynomials with rational coefficients.
range over the polynomials with rational coefficients.
Comments
An algebraic number field 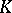 of degree
of degree  is an extension of degree
is an extension of degree  of the field
of the field 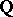 of rational numbers. Alternatively, a number field
of rational numbers. Alternatively, a number field 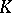 is an algebraic number field (of degree
is an algebraic number field (of degree  ) if every
) if every 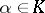 is the root of a polynomial (of degree at most
is the root of a polynomial (of degree at most  ) over
) over 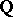 . A number field that is not algebraic is called transcendental. (Cf. also Algebraic number theory; Extension of a field; Transcendental extension.)
. A number field that is not algebraic is called transcendental. (Cf. also Algebraic number theory; Extension of a field; Transcendental extension.)
References
| [a1] | E. Weiss, "Algebraic number theory" , McGraw-Hill (1963) pp. Sects. 4–9 |
Number field. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Number_field&oldid=14270