Montmort matching problem
From Encyclopedia of Mathematics
derangement problem
Take two sets, 
and 
, and a bijection, 
, between them. (E.g., take 
married couples and let 
be the set of husbands and 
the set of wives.) Now, take a random paring (a bijection again). What is the chance that this random pairing gives at least one "correct match" (i.e. coincides with 
in at least one element). Asymptotically, this probability is 
. This follows immediately from the formula given in Classical combinatorial problems for the number of permutations 
such that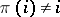 
for all 
.
This problem was considered first by P.R. de Montmort (around 1700) in connection with a card game known as the "jeu du treize" , "jeu de rencontre" or simply "rencontre" .
References
| [a1] | E. Knobloch, "Euler and the history of a problem in probability theory" Ganita–Bharati , 6 (1984) pp. 1–12 |
How to Cite This Entry:
Montmort matching problem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Montmort_matching_problem&oldid=14268
Montmort matching problem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Montmort_matching_problem&oldid=14268
This article was adapted from an original article by M. Hazewinkel (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article