Ring of polynomials
polynomial ring
A ring whose elements are polynomials (cf. Polynomial) with coefficients in some fixed field  . Rings of polynomials over an arbitrary commutative associative ring
. Rings of polynomials over an arbitrary commutative associative ring 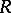 , for example, over the ring of integers, are also discussed. The accepted notation for the ring of polynomials in a finite set of variables
, for example, over the ring of integers, are also discussed. The accepted notation for the ring of polynomials in a finite set of variables  over
over 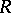 is
is  . It is possible to speak of a ring of polynomials in an infinite set of variables if it is assumed that each individual polynomial depends only on a finite number of variables. A ring of polynomials over a ring
. It is possible to speak of a ring of polynomials in an infinite set of variables if it is assumed that each individual polynomial depends only on a finite number of variables. A ring of polynomials over a ring 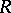 is a (commutative) free algebra with an identity over
is a (commutative) free algebra with an identity over 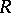 ; the set of variables serves as a system of free generators of this algebra.
; the set of variables serves as a system of free generators of this algebra.
A ring of polynomials over an arbitrary integral domain is itself an integral domain. A ring of polynomials over a factorial ring is itself factorial.
For a ring of polynomials in a finite number of variables over a field 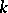 there is Hilbert's basis theorem: Every ideal in
there is Hilbert's basis theorem: Every ideal in 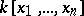 is finitely generated (as an ideal) (cf. Hilbert theorem). A ring of polynomials in one variable over a field,
is finitely generated (as an ideal) (cf. Hilbert theorem). A ring of polynomials in one variable over a field,  is a principal ideal ring, that is, each ideal of it is generated by one element. Moreover,
is a principal ideal ring, that is, each ideal of it is generated by one element. Moreover, 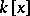 is a Euclidean ring. This property of
is a Euclidean ring. This property of 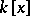 gives one the possibility of comprehensively describing the finitely-generated modules over it and, in particular, of reducing linear operators in a finite-dimensional vector space to canonical form (see Jordan matrix). For
gives one the possibility of comprehensively describing the finitely-generated modules over it and, in particular, of reducing linear operators in a finite-dimensional vector space to canonical form (see Jordan matrix). For 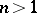 the ring
the ring 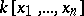 is not a principal ideal ring.
is not a principal ideal ring.
Let 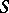 be a commutative associative
be a commutative associative 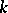 -algebra with an identity, and let
-algebra with an identity, and let 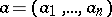 be an element of the Cartesian power
be an element of the Cartesian power 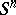 . Then there is a unique
. Then there is a unique  -algebra homomorphism of the ring of polynomials in
-algebra homomorphism of the ring of polynomials in  variables into
variables into  ,
,
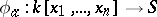 |
for which 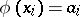 , for all
, for all 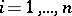 , and
, and 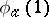 is the identity of
is the identity of 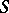 . The image of a polynomial
. The image of a polynomial 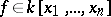 under this homomorphism is called its value at the point
under this homomorphism is called its value at the point  . A point
. A point 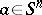 is called a zero of a system of polynomials
is called a zero of a system of polynomials 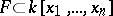 if the value of each polynomial from
if the value of each polynomial from 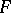 at this point is
at this point is  . For a ring of polynomials there is Hilbert's Nullstellen Satz: Let
. For a ring of polynomials there is Hilbert's Nullstellen Satz: Let 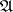 be an ideal in the ring
be an ideal in the ring 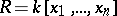 , let
, let  be the set of zeros of
be the set of zeros of 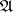 in
in 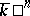 , where
, where 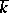 is the algebraic closure of
is the algebraic closure of 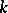 , and let
, and let 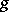 be a polynomial in
be a polynomial in  vanishing at all points of
vanishing at all points of 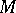 . Then there is a natural number
. Then there is a natural number  such that
such that 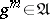 (cf. Hilbert theorem).
(cf. Hilbert theorem).
Let 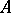 be an arbitrary module over the ring
be an arbitrary module over the ring 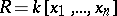 . Then there are free
. Then there are free 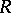 -modules
-modules 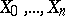 and homomorphisms
and homomorphisms 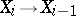 such that the sequence of homomorphisms
such that the sequence of homomorphisms
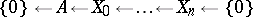 |
is exact, that is, the kernel of one homomorphism is the image of the next. This result is one possible formulation of the Hilbert theorem on syzygies for a ring of polynomials.
A finitely-generated projective module over a ring of polynomials in a finite number of variables with coefficients from a principal ideal ring is free (see [5], [6]); this is the solution of Serre's problem.
Only in certain particular cases are there answers to the following questions: 1) Is the group of automorphisms of a ring of polynomials generated by elementary automorphisms? 2) Is 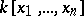 generated by some set
generated by some set 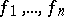 for which
for which  is a non-zero constant? 3) If
is a non-zero constant? 3) If 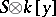 is isomorphic to
is isomorphic to 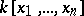 , must
, must 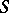 be isomorphic to
be isomorphic to 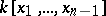 ?
?
References
| [1] | S. Lang, "Algebra" , Addison-Wesley (1974) |
| [2] | N. Bourbaki, "Algèbre" , Eléments de mathématiques , 2 , Masson (1981) pp. Chapts. 4; 5; 6 |
| [3] | D. Hilbert, "Ueber die vollen Invariantensysteme" Math. Ann. , 42 (1893) pp. 313–373 |
| [4] | D. Hilbert, "Ueber die Theorie der algebraischen Formen" Math. Ann. , 36 (1890) pp. 473–534 |
| [5] | A.A. Suslin, "Projective modules over a polynomial ring are free" Soviet Math. Dokl. , 17 : 4 (1976) pp. 1160–1164 Dokl. Akad. Nauk SSSR , 229 (1976) pp. 1063–1066 |
| [6] | D. Quillen, "Projective modules over polynomial rings" Invent. Math. , 36 (1976) pp. 167–171 |
Ring of polynomials. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Ring_of_polynomials&oldid=14262