Epidemic process
From Encyclopedia of Mathematics
A random process (cf. Stochastic process) that serves as a mathematical model of the spread of some epidemy. One of the simplest such models can be described as a continuous-time Markov process whose states at the moment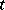 
are the number 
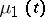of sick persons and the number 
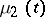of exposed persons. If 
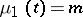and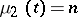 
, then at the time 
, 
, 
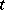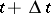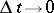, the transition probability is determined as follows: 
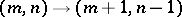with probability 
; 
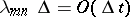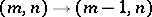with probability 
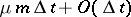. In this case the generating function
 |
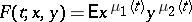satisfies the differential equation
 |
Comments
References
| [a1] | N.T.J. Bailey, "The mathematical theory of infections diseases and its applications" , Hafner (1975) |
| [a2] | D. Ludwig, "Stochastic population theories" , Springer (1974) |
How to Cite This Entry:
Epidemic process. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Epidemic_process&oldid=14259
Epidemic process. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Epidemic_process&oldid=14259
This article was adapted from an original article by B.A. Sevast'yanov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article