Pfaffian

of a skew-symmetric matrix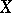

The polynomial 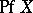in the entries of 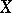whose square is 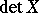. More precisely, if 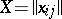is a skew-symmetric matrix (i.e. 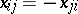, 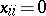; such a matrix is sometimes also called an alternating matrix) of order 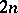over a commutative-associative ring 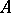with a unit, then 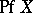is the element of 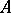given by the formula

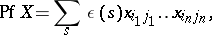where the summation is over all possible partitions of the set 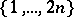into non-intersecting pairs 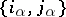, where one may suppose that 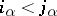, , 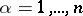and where is the sign of the permutation

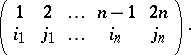A Pfaffian has the following properties:

1) 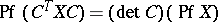for any matrix 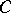of order ;

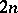2) ;

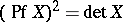3) if 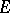is a free 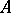-module with basis 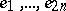and if

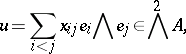then

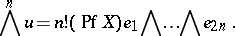References

[1]	N. Bourbaki, "Elements of mathematics. Algebra: Modules. Rings. Forms" , 2 , Addison-Wesley (1975) pp. Chapt.4;5;6 (Translated from French)