Titchmarsh-Weyl m-function
A function arising in an attempt to properly determine which singular boundary-value problems are self-adjoint (cf. also Self-adjoint differential equation). Begin with a formally symmetric differential expression
 |
where 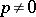 ,
, 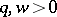 are measurable coefficients over
are measurable coefficients over  , and which is defined on a domain within
, and which is defined on a domain within 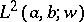 . The Titchmarsh–Weyl
. The Titchmarsh–Weyl 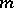 -function is defined as follows: For
-function is defined as follows: For  ,
, 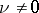 , let
, let 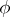 and
and 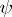 be solutions of
be solutions of 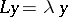 satisfying
satisfying
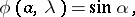 |
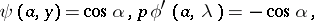 |
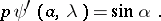 |
Now consider a real boundary condition at 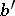 ,
, 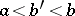 , of the form
, of the form
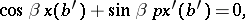 |
and let  satisfy it. Then
satisfy it. Then
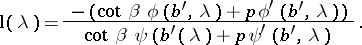 |
If 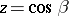 ,
, 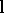 is a meromorphic function in the complex
is a meromorphic function in the complex  -plane; indeed, it is a bilinear transformation. As
-plane; indeed, it is a bilinear transformation. As  varies over real values
varies over real values 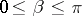 ,
,  varies over the real
varies over the real  -axis, and
-axis, and 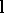 describes a circle in the
describes a circle in the  -plane.
-plane.
It can be shown that if 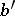 increases, the circles become nested. Hence there is at least one point inside all. For such a point
increases, the circles become nested. Hence there is at least one point inside all. For such a point 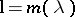 ,
,
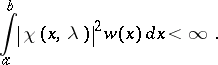 |
There exists at least one solution of 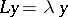 , which is square-integrable.
, which is square-integrable.
If the limit of the circles is a point, then 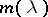 is unique and only
is unique and only 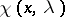 is square-integrable. This is the limit-point case. If the limit of the circles is itself a circle, then
is square-integrable. This is the limit-point case. If the limit of the circles is itself a circle, then 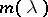 is not unique and all solutions of
is not unique and all solutions of 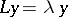 are square-integrable. This is the limit-circle case.
are square-integrable. This is the limit-circle case.
Nonetheless, the differential operator
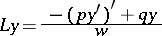 |
whose domain satisfies
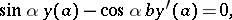 |
 |
where 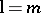 on the limit circle or limit point, is a self-adjoint differential operator (cf. also Self-adjoint operator; Self-adjoint differential equation) on
on the limit circle or limit point, is a self-adjoint differential operator (cf. also Self-adjoint operator; Self-adjoint differential equation) on 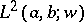 .
.
If the circle limit is a point, the second boundary condition (at 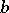 ) is automatic.
) is automatic.
The spectral measure of 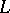 is given by
is given by
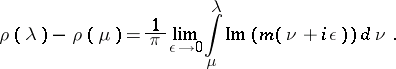 |
The spectral resolution of arbitrary functions in 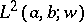 is
is
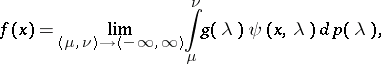 |
where the limit is in the mean-square sense, and
 |
References
| [a1] | E.A. Coddington, N. Levinson, "Theory of ordinary differential equations" , McGraw-Hill (1955) |
| [a2] | A.M. Krall, " theory for singular Hamiltonian systems with one singular point" SIAM J. Math. Anal. , 20 (1989) pp. 644–700 theory for singular Hamiltonian systems with one singular point" SIAM J. Math. Anal. , 20 (1989) pp. 644–700 |
Titchmarsh-Weyl m-function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Titchmarsh-Weyl_m-function&oldid=14178