Brelot harmonic space
Roughly speaking, a Brelot harmonic space is a locally compact space endowed with an additional structure making it possible to study notions known from classical potential theory, such as harmonic and hyperharmonic functions, potentials, minimum principle, the Dirichlet problem, harmonic measure, balayage, fine topology, Martin compactification, etc. Standard examples are provided by elliptic partial differential equations in Euclidean spaces or on manifolds or by harmonic functions on a Riemann surface. (Cf. also Harmonic space; Potential theory, abstract.)
Let  be a locally compact, locally connected topological space and let
be a locally compact, locally connected topological space and let  be a sheaf of vector spaces of real-valued continuous functions. This means that to every non-empty open set
be a sheaf of vector spaces of real-valued continuous functions. This means that to every non-empty open set  , a vector space
, a vector space  consisting of continuous functions on
consisting of continuous functions on  is associated in such a way that: i) if
is associated in such a way that: i) if  ,
,  is a non-empty open set, then the restriction
is a non-empty open set, then the restriction  ; and ii) if
; and ii) if 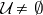 is a family of non-empty open sets with union
is a family of non-empty open sets with union  and
and 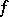 is a function on
is a function on  such that
such that 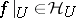 for every
for every 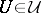 , then
, then 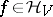 . (The elements of
. (The elements of 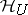 are called harmonic functions on
are called harmonic functions on 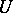 with respect to
with respect to 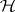 ; cf. also Harmonic function.)
; cf. also Harmonic function.)
The sheaf 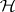 is called a Brelot harmonic structure (the terminology from [a1]) if the following three axioms hold:
is called a Brelot harmonic structure (the terminology from [a1]) if the following three axioms hold:
I)  is not degenerate, i.e., for every
is not degenerate, i.e., for every  there exists an open neighbourhood
there exists an open neighbourhood 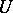 of
of  and a strictly positive function
and a strictly positive function 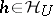 ;
;
II) (the base axiom) the topology of 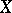 has a basis consisting of regular sets. (Here, a set
has a basis consisting of regular sets. (Here, a set 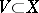 is said to be regular (with respect to
is said to be regular (with respect to 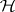 ) if the Dirichlet problem on
) if the Dirichlet problem on 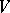 is solvable in the following sense: For every real-valued continuous function
is solvable in the following sense: For every real-valued continuous function 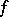 on the boundary of
on the boundary of 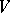 , there exists a uniquely determined harmonic function
, there exists a uniquely determined harmonic function 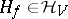 which extends
which extends 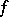 continuously. Furthermore,
continuously. Furthermore, 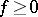 implies
implies 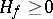 .)
.)
III) the Brelot convergence axiom: for every increasing sequence 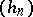 of harmonic functions on a domain
of harmonic functions on a domain 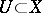 one has
one has 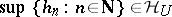 , provided that
, provided that 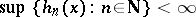 for some
for some 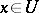 .
.
The pair 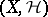 is then called a Brelot harmonic space. (These spaces were introduced by M. Brelot in 1957; see [a3]. Later on, more general axiomatic settings for potential theory were developed, mainly by H. Bauer, C. Constantinescu and A. Cornea, J. Bliedtner and W. Hansen, N. Boboc, Gh. Bucur and Cornea; see [a1] and [a2].)
is then called a Brelot harmonic space. (These spaces were introduced by M. Brelot in 1957; see [a3]. Later on, more general axiomatic settings for potential theory were developed, mainly by H. Bauer, C. Constantinescu and A. Cornea, J. Bliedtner and W. Hansen, N. Boboc, Gh. Bucur and Cornea; see [a1] and [a2].)
Results of J.M. Bony (see e.g. [a1]) show that, in a sense, the theory of Brelot harmonic spaces is close to potential theory for second-order partial differential equations of elliptic type (cf. also Potential theory, abstract). A great deal of results known from classical potential theory (which corresponds to the Laplace equation) can be obtained in the framework of Brelot harmonic spaces; sometimes additional hypotheses are imposed. Moreover, there is an important and deep connection between a class of Markov processes and Brelot harmonic spaces (see [a1] and [a2] and Markov process).
References
| [a1] | H. Bauer, "Harmonic spaces; a survey" Conf. Sem. Mat. Univ. Bari , 197 (1984) |
| [a2] | J. Bliedtner, W. Hansen, "Potential theory; an analytic and probabilistic approach to balayage" , Springer (1986) |
| [a3] | M. Brelot, "Axiomatique des fonctions harmoniques" , Presses Univ. Montréal (1966) |
Brelot harmonic space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Brelot_harmonic_space&oldid=14164