Quantile
One of the numerical characteristics of a probability distribution. For a real random variable 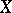 with distribution function
with distribution function 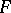 , by a quantile of order
, by a quantile of order 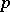 ,
, 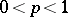 , one means the number
, one means the number 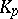 for which
for which 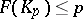 ,
, 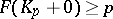 . If
. If 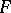 is a continuous strictly-monotone function, then
is a continuous strictly-monotone function, then 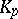 is the unique solution of the equation
is the unique solution of the equation 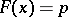 , that is,
, that is, 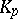 is the function of
is the function of 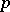 inverse to the function
inverse to the function 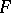 . If
. If 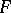 is continuous and
is continuous and 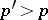 , then the probability of the inequality
, then the probability of the inequality 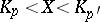 , is equal to
, is equal to 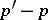 . The quantile
. The quantile 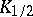 is the median (in statistics) of the random variable
is the median (in statistics) of the random variable 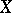 . The quantiles
. The quantiles 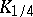 and
and 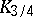 are called the quartiles, and
are called the quartiles, and 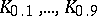 , the deciles. The values of the quantiles for suitable values of
, the deciles. The values of the quantiles for suitable values of 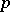 enable one to form an idea about the distribution function.
enable one to form an idea about the distribution function.
For example, for the normal distribution (see Fig.)
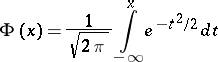 |
the graph of the function 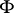 can be drawn from the deciles:
can be drawn from the deciles: 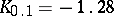 ;
; 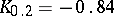 ;
; 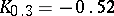 ;
; 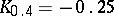 ;
; 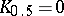 ;
; 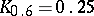 ;
; 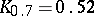 ;
; 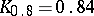 ;
; 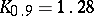 .
.
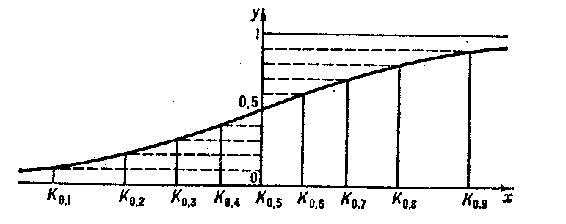
Figure: q076270a
The quartiles of the normal distribution 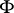 are
are 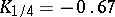 and
and 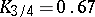 .
.
Comments
References
| [a1] | L. Breiman, "Statistics" , Houghton Mifflin (1973) pp. 231ff |
| [a2] | H. Cramér, "Mathematical methods of statistics" , Princeton Univ. Press (1946) pp. 181; 367 |
Quantile. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Quantile&oldid=14159