Bessel potential operator
A classical Bessel potential operator is a generalized convolution operator (or a pseudo-differential operator)
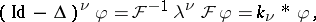 |
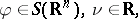 |
with symbol
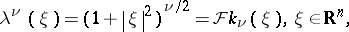 |
where 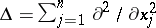 is the Laplace operator,
is the Laplace operator, 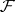 and
and 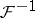 are, respectively, the Fourier transform and its inverse, and
are, respectively, the Fourier transform and its inverse, and 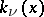 is a generalized kernel (cf. also Kernel of an integral operator). If
is a generalized kernel (cf. also Kernel of an integral operator). If 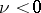 , the kernel
, the kernel 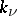 is the modified Bessel function of the third kind (cf. also Bessel functions) and
is the modified Bessel function of the third kind (cf. also Bessel functions) and
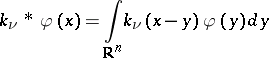 |
is an ordinary convolution of functions [a1], [a2], [a5].
The set of functions
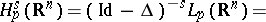 |
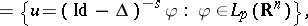 |
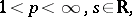 |
is known as the Bessel potential space.
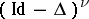 extends to an isomorphism between the Bessel potential spaces:
extends to an isomorphism between the Bessel potential spaces: 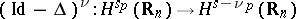 [a1], [a2], [a5], and even between more general Besov–Triebel–Lizorkin spaces
[a1], [a2], [a5], and even between more general Besov–Triebel–Lizorkin spaces 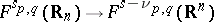 [a6].
[a6].
Now, let 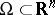 be a special Lipschitz domain. A linear operator
be a special Lipschitz domain. A linear operator 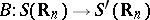 is said to be a Bessel potential operator of order
is said to be a Bessel potential operator of order 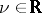 for
for  (briefly written as
(briefly written as 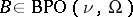 ) if [a3]:
) if [a3]:
i) 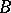 is translation invariant:
is translation invariant: 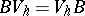 with
with 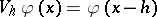 ,
, 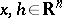 ;
;
ii) there exists a continuous and invertible extension 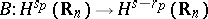 for all
for all 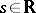 ,
, 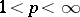 ;
;
iii) 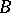 and its inverse
and its inverse 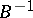 preserve supports within
preserve supports within 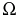 :
: 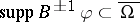 , provided
, provided 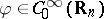 and
and 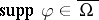 (here,
(here, 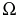 stands for the closure of
stands for the closure of  ).
).
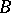 is said to be a Bessel potential operator for
is said to be a Bessel potential operator for  (briefly,
(briefly, 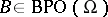 ) if
) if 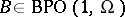 and if it generates an additive group
and if it generates an additive group 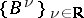 ,
, 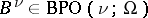 ,
, 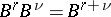 ,
, 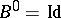 [a3].
[a3].
The following assertions are basic for Bessel potential operators.
1) For a special Lipschitz domain 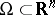 the inclusion
the inclusion 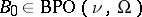 holds if and only if
holds if and only if
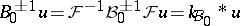 |
is a generalized convolution, with
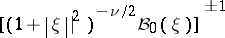 |
being 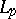 -multipliers (cf. also Multiplier theory) and
-multipliers (cf. also Multiplier theory) and 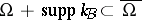 [a3].
[a3].
The group of 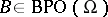 can be generated as follows:
can be generated as follows: 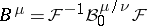 for
for 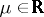 [a3].
[a3].
2) Let  ,
,  and
and 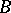 be as in 1). There exists a generalized kernel
be as in 1). There exists a generalized kernel 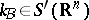 such that
such that 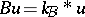 for all
for all 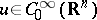 ; if
; if 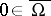 , then
, then 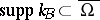 .
.
If 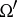 is another special Lipschitz domain and
is another special Lipschitz domain and 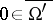 ,
, 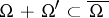 , then
, then 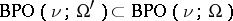 for all
for all 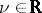 [a3].
[a3].
3) Let 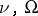 be as in 1). Any operator
be as in 1). Any operator 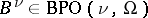 arranges an isomorphism
arranges an isomorphism 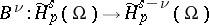 of the Bessel potential spaces of functions vanishing at the boundary
of the Bessel potential spaces of functions vanishing at the boundary
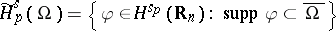 |
(the same for the 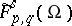 -spaces).
-spaces).
4) Let  be as in 1) and let, further,
be as in 1) and let, further,  be the restriction and let
be the restriction and let 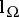 be one of its right inverses,
be one of its right inverses, 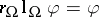 for
for 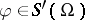 . Then the restricted adjoint operator
. Then the restricted adjoint operator 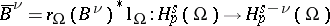 arranges an isomorphism, where
arranges an isomorphism, where 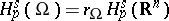 . The isomorphism is independent of the choice of a right inverse
. The isomorphism is independent of the choice of a right inverse 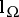 (the same for the
(the same for the 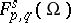 -spaces).
-spaces).
5) For all 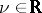 and any general Lipschitz domain
and any general Lipschitz domain 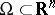 (even for a manifold
(even for a manifold  with a Lipschitz boundary) there exist pseudo-differential operators
with a Lipschitz boundary) there exist pseudo-differential operators 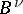 and
and  such that
such that 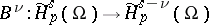 and
and 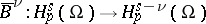 will be isomorphisms (the same for the
will be isomorphisms (the same for the 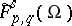 - and
- and 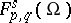 -spaces).
-spaces). 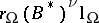 is independent of the choice of
is independent of the choice of 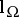 . If
. If 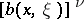 is the principal symbol of
is the principal symbol of 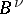 (cf. also Symbol of an operator), then
(cf. also Symbol of an operator), then 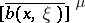 will be the principal symbol of
will be the principal symbol of 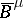 .
. 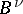 can be chosen, among others, with principal symbols from the Hörmander class
can be chosen, among others, with principal symbols from the Hörmander class 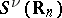 [a3], [a4].
[a3], [a4].
6) The operators 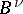 and
and 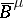 from the above assertion can be applied to the lifting of pseudo-differential operators (i.e. to reduction of the order): if
from the above assertion can be applied to the lifting of pseudo-differential operators (i.e. to reduction of the order): if 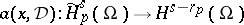 is a pseudo-differential operator with principal symbol
is a pseudo-differential operator with principal symbol 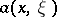 , then
, then 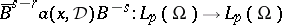 will be an equivalent pseudo-differential operator, with principal symbol
will be an equivalent pseudo-differential operator, with principal symbol 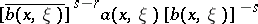 [a3], [a4].
[a3], [a4].
References
| [a1] | N. Aronszajn, K. Smith, "Theory of Bessel potentials, Part 1" Ann. Inst. Fourier , 11 (1961) pp. 385–475 |
| [a2] | A.P. Calderón, "Lebesque spaces of differentiable functions and distributions" C.B. Morrey (ed.) , Partial Differential Equations , Amer. Math. Soc. (1961) pp. 33–49 |
| [a3] | R. Duduchava, F.-O. Speck, "Pseudo-differential operators on compact manifolds with Lipschitz boundary" Math. Nachr. , 160 (1993) pp. 149–191 |
| [a4] | R. Schneider, "Bessel potential operators for canonical Lipschitz domains" Math. Nachr. , 150 (1991) pp. 277–299 |
| [a5] | E. Stein, "Singular integrals and differentiability properties of functions" , Princeton Univ. Press (1970) |
| [a6] | H. Triebel, "Interpolation theory, function spaces, differential operators" , North-Holland (1978) |
| [a7] | R. Schneider, "Reduction of order for pseudodifferential operators on Lipschitz domains" Comm. Partial Diff. Eq. , 18 (1991) pp. 1263–1286 |
Bessel potential operator. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Bessel_potential_operator&oldid=14142