Quasi-cyclic group

group of type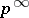

An infinite Abelian 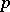-group all proper subgroups of which are cyclic (cf. Cyclic group). There exists for each prime number 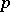a quasi-cyclic group, and it is unique up to an isomorphism. This group is isomorphic to the multiplicative group of all roots of the equations

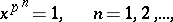in the field of complex numbers with the usual multiplication, and also to the quotient group 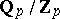, where 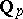is the additive group of the field of rational 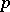-adic numbers and 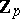is the additive group of the ring of all 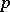-adic integers. A quasi-cyclic group is the union of an ascending chain of cyclic groups 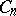of orders 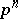, 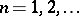; more precisely, it is the inductive limit

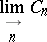with respect to the inductive system 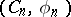. This group can be defined in terms of generators and relations as the group with countable system of generators 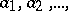and relations

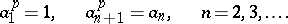Quasi-cyclic groups are the only infinite Abelian (and also the only locally-finite infinite) groups all subgroups of which are finite. The question of the existence of infinite non-Abelian groups with this property is still unsolved (1978) and constitutes one of the problems of O.Yu. Shmidt.

Quasi-cyclic groups are divisible Abelian groups (cf. Divisible group), and each divisible Abelian group is the direct sum of a set of groups that are isomorphic to the additive group of rational numbers and to quasi-cyclic groups for certain prime numbers 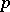. Groups of type 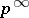are maximal 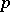-subgroups of the multiplicative group of complex numbers, and also maximal 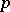-subgroups of the additive group of rational numbers modulo 1. The ring of endomorphisms of a group of type 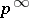is isomorphic to the ring of 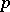-adic integers. A quasi-cyclic group coincides with its Frattini subgroup.

References

[1]	A.G. Kurosh, "The theory of groups" , 1–2 , Chelsea (1955–1956) (Translated from Russian)
[2]	M.I. Kargapolov, J.I. [Yu.I. Merzlyakov] Merzljakov, "Fundamentals of the theory of groups" , Springer (1979) (Translated from Russian)

Comments

A quasi-cyclic group is better known as a Prüfer group in the West.