Heisenberg representation

One of the principal possible equivalent representations (together with the Schrödinger representation and the representation of interaction, cf. Interaction, representation of) of the dependence of the operators 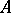and the wave functions 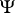on the time 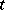in quantum mechanics and in quantum field theory. 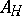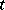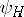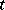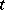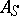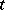In the Heisenberg representation the operators depend on , while the wave functions do not depend on , and are connected with the corresponding -independent operators and -dependent wave functions 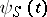in the Schrödinger representation by a unitary transformation

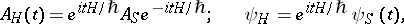(1)

where the Hermitian operator 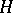is the complete Hamiltonian of the system, which is independent of time. That it is possible to introduce the Heisenberg representation, the Schrödinger representation and the representation of interaction, and that they are equivalent, is due to the fact that it is not 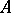or 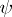by themselves but only the average value of the operators 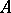in the state 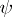that must be invariant with respect to unitary transformations of the type (1) and, consequently, the average value should not depend on the selection of the representation. Differentiation of (1) with respect to yields an equation for the operators 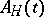in the Heisenberg representation that contains complete information on the variation of the state of the quantum system with the time :

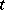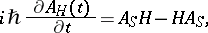where the operators 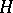and 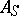do not usually commute.

Named after W. Heisenberg, who introduced it in 1925 in a matrix formulation of quantum mechanics.

References

[a1]	J. Mehra, H. Rechenberg, "The historical development of quantum theory" , 1–4 , Springer (1982)