Approximation by periodic transformations

One of the methods of ergodic theory. Any automorphism 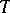of a Lebesgue space 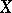with measure 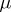can be obtained as the limit of periodic automorphisms 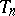in the natural weak or uniform topology of the space 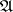of all automorphisms [1]. To characterize the rate of approximation quantitatively one considers not only the automorphisms 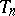, but also finite measurable decompositions of 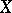which are invariant under 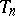, i.e. decompositions of 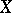into a finite number of non-intersecting measurable sets 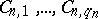, which are mapped into each other by 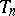. The number

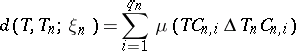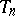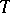is an estimate of the proximity of to with respect to 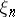; here 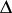is the symmetric difference

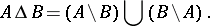If 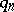is given, it is possible to choose 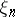and 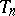(with the above properties) such that 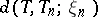is arbitrarily small [1]. The metric invariants of the automorphism 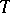become apparent on considering infinite sequences 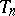and 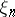such that for any measurable set 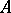there exists a sequence of sets 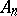, each being the union of some of the 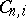, which approximates 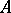in the sense that

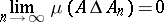( "the decompositions xn converge to a decomposition into points" ). If, in addition, 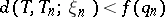, where 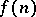is a given monotone sequence tending to zero, then one says that 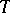admits an approximation of the first type by periodic transformations with rate 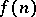; if, in addition, 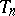permutes the sets 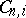cyclically, then one speaks of cyclic approximation by periodic transformations. For other variants see [2], [6], [7].

At a certain rate of approximation certain properties of the periodic automorphisms 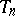affect the properties of the limit automorphism 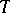. Thus, if 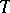has a cyclic approximation by periodic transformations with a rate 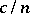, then, if 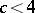, 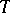will be ergodic; if 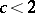, 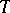will not be mixing; and if 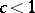, the spectrum of the corresponding unitary shift operator is simple. Certain properties of 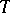may be described in terms of the rate of approximation. Thus, its entropy is equal to the lower bound of the 's for which 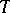admits an approximation by periodic transformations of the first kind with a rate of 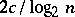[2], [7]. Approximations by periodic transformations were used in the study of a number of simple examples [2], including smooth flows on two-dimensional surfaces [8]. They served in the construction of a number of dynamical systems with unexpected metric properties [2], [6], [7], or with an unexpected combination of metric and differential properties [3], [4].

The statement on the density of periodic automorphisms in 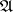, provided with the weak topology, may be considerably strengthened: For any monotone sequence 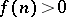, the automorphisms which allow cyclic approximations at the rate 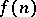form a set of the second category in 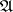[2]. Accordingly, approximations by periodic transformations yield so-called category theorems, which state that in 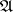(with the weak topology) the automorphisms with a given property form a set of the first or second category (e.g. ergodic sets are of the second category, while mixing sets are of the first category [1]).

Let 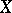be a topological or smooth manifold, and let the measure 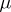be compatible with the topology or with the differential structure. In the class of homeomorphisms or diffeomorphisms preserving 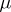it is not the weak topology, but other topologies that are natural. Category theorems analogous to those for 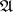are valid for homeomorphisms; for the history of the problem and its present "state-of-the-art" see [5].

References

[1]	P.R. Halmos, "Lectures on ergodic theory" , Math. Soc. Japan (1956)
[2]	A.B. Katok, A.M. Stepin, "Approximations in ergodic theory" Russian Math. Surveys , 22 : 5 (1967) pp. 77–102 Uspekhi Mat. Nauk , 22 : 5 (1967) pp. 81–106
[3]	D.V. Anosov, A.B. Katok, "New examples in smooth ergodic theory. Ergodic diffeomorphisms" Trans. Moscow Math. Soc. , 23 (1970) pp. 3–36 Trudy Moskov. Mat. Obshch. , 23 (1970) pp. 1–35
[4]	A.B. Katok, "Ergodic perturbations of degenerate integrable Hamiltonian systems" Math. USSR-Izv. , 7 : 3 (1973) pp. 535–571 Izv. Akad. Nauk SSSR Ser. Mat. , 37 (1973) pp. 539–576
[5]	A.B. Katok, A.M. Stepin, "Metric properties of measure preserving homeomorphisms" Russian Math. Surveys , 25 : 2 (1970) pp. 191–220 Uspekhi Mat. Nauk , 25 : 2 (1970) pp. 193–220
[6]	M.A. Akcoglu, R.V. Chacon, T. Schwartzbauer, "Commuting transformations and mixing" Proc. Amer. Math. Soc. , 24 pp. 637–642
[7]	T. Schwartzbauer, "Entropy and approximation of measure preserving transformations" Pacific J. Math. , 43 (1972) pp. 753–764
[8]	A.V. Kochergin, "On mixing in special flows over a shifting of segments and in smooth flows on surfaces" Math. USSR-Sb. , 25 : 3 (1975) pp. 441–469 Mat. Sb. , 96 : 3 (1975) pp. 472–502

Comments

Contributions to the foundation of the theory of approximations were also made by V.A. Rokhlin (cf. [a2]).

If in an approximation by periodic transformations one has the following inequality for the sequences 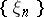, , 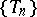where 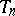is periodic of order ,

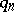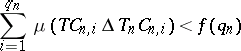and 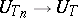in the strong topology for operators on 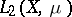, then one says that 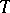admits an approximation of the second type by periodic transformations with speed 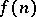. Reference [a1] is a basic and well-known one.

In this context one also speaks of partitions instead of decompositions.

References

[a1]	I.P. [I.P. Kornfel'd] Cornfel'd, S.V. Fomin, Ya.G. Sinai, "Ergodic theory" , Springer (1982) pp. Chapt. 15;16 (Translated from Russian)
[a2]	V.A. Rokhlin, "Selected topics from the metric theory of dynamical systems" Amer. Math. Soc. Transl. Series 2 , 49 pp. 171–240 Uspekhi Mat. Nauk , 4 : 2 (30) (1949) pp. 57–128