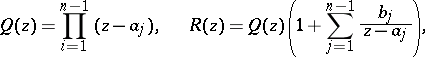A linear ordinary differential equation of order  of the form
of the form
where  is a complex constant and
is a complex constant and  are polynomials of degree
are polynomials of degree  and
and  , respectively. The Pochhammer equation was studied by L. Pochhammer [1] and C. Jordan [2].
, respectively. The Pochhammer equation was studied by L. Pochhammer [1] and C. Jordan [2].
The Pochhammer equation has been integrated using the Euler transformation, and its particular integrals have the form
 | (*) |
where  is some contour in the complex
is some contour in the complex 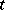 -plane. Let all roots
-plane. Let all roots 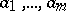 of the polynomial
of the polynomial 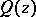 be simple and let the residues of
be simple and let the residues of 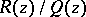 at these points be non-integers. Let
at these points be non-integers. Let  be a fixed point such that
be a fixed point such that 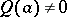 and let
and let 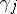 be a simple closed curve with origin and end at
be a simple closed curve with origin and end at  , positively oriented and containing only the root
, positively oriented and containing only the root  ,
, 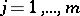 , inside it. Formula (*) gives the solution of the Pochhammer equation, if with
, inside it. Formula (*) gives the solution of the Pochhammer equation, if with
exactly 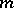 of these solutions are linearly independent. To construct the other solutions other contours are used, including non-closed ones (see [3], [4]). The monodromy group for the Pochhammer equation has been calculated (see [3]).
of these solutions are linearly independent. To construct the other solutions other contours are used, including non-closed ones (see [3], [4]). The monodromy group for the Pochhammer equation has been calculated (see [3]).
Particular cases of the Pochhammer equation are the Tissot equation (see [4]), i.e. the Pochhammer equation in which
and the Papperitz equation.
References
| [1] | L. Pochhammer, "Ueber ein Integral mit doppeltem Umlauf" Math. Ann. , 35 (1889) pp. 470–494 |
| [2] | C. Jordan, "Cours d'analyse" , 3 , Gauthier-Villars (1915) |
| [3] | E.L. Ince, "Ordinary differential equations" , Dover, reprint (1956) |
| [4] | E. Kamke, "Handbuch der gewöhnliche Differentialgleichungen" , Chelsea, reprint (1947) |
How to Cite This Entry:
Pochhammer equation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Pochhammer_equation&oldid=14095
This article was adapted from an original article by M.V. Fedoryuk (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098.
See original article of the form
of the form

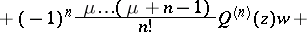
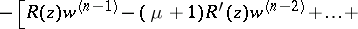
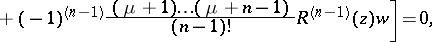
 is a complex constant and
is a complex constant and  are polynomials of degree
are polynomials of degree  and
and  , respectively. The Pochhammer equation was studied by L. Pochhammer [1] and C. Jordan [2].
, respectively. The Pochhammer equation was studied by L. Pochhammer [1] and C. Jordan [2].

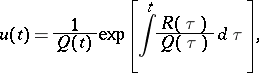
 is some contour in the complex
is some contour in the complex 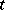 -plane. Let all roots
-plane. Let all roots 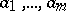 of the polynomial
of the polynomial 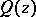 be simple and let the residues of
be simple and let the residues of 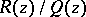 at these points be non-integers. Let
at these points be non-integers. Let  be a fixed point such that
be a fixed point such that 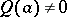 and let
and let 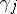 be a simple closed curve with origin and end at
be a simple closed curve with origin and end at  , positively oriented and containing only the root
, positively oriented and containing only the root  ,
, 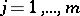 , inside it. Formula (*) gives the solution of the Pochhammer equation, if with
, inside it. Formula (*) gives the solution of the Pochhammer equation, if with
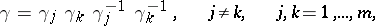
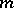 of these solutions are linearly independent. To construct the other solutions other contours are used, including non-closed ones (see [3], [4]). The monodromy group for the Pochhammer equation has been calculated (see [3]).
of these solutions are linearly independent. To construct the other solutions other contours are used, including non-closed ones (see [3], [4]). The monodromy group for the Pochhammer equation has been calculated (see [3]).