Lyapunov stability

of a point relative to a family of mappings

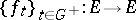of a certain space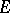

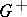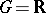Equicontinuity of this family of mappings at the point (here is the set of non-negative numbers in ; for example, the real numbers or the integers ). Lyapunov stability of a point relative to the family of mappings

is equivalent to the continuity at this point of the mapping 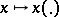of a neighbourhood of this point into the set of functions 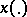defined by the formula 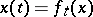, equipped with the topology of uniform convergence on . Lyapunov stability of a point relative to a mapping is defined as Lyapunov stability relative to the family of non-negative powers of this mapping. Lyapunov stability of a point relative to a dynamical system is Lyapunov stability of this point relative to the family 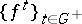. Lyapunov stability of the solution 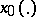of an equation 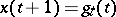given on 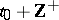is Lyapunov stability of the point 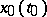relative to the family of mappings .

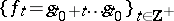Lyapunov stability of the solution 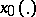of a differential equation 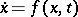given on 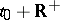is Lyapunov stability of the point 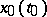relative to the family of mappings 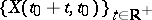, where 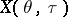is the Cauchy operator of this equation. Lyapunov stability of the solution 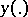of a differential equation

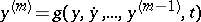of order 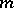, given on 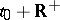, is Lyapunov stability of the solution 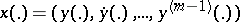of the corresponding first-order differential equation 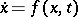, given on 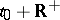, where

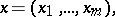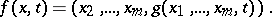The definitions 1–7 given below are some concrete instances of the above and related definitions.

1) Let a differential equation 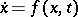be given, where lies in an -dimensional normed space 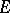. A solution 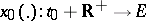of this equation is called Lyapunov stable if for every 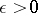there exists a 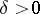such that for every satisfying the inequality 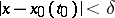, the solution 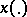of the Cauchy problem

is unique, defined on 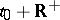, and for each 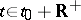satisfies the inequality 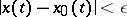. If, in addition, one can find a 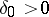such that for every solution 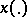of the equation 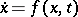whose initial value satisfies the inequality

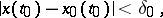the equation

holds (respectively, the inequality

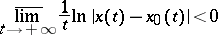holds; here and elsewhere one puts 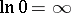), then the solution 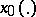is called asymptotically (respectively, exponentially) stable.

A solution of the equation

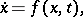(2)

where or 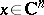, is called Lyapunov stable (asymptotically, exponentially stable) if it becomes such after equipping the space 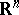(or 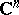) with a norm. This property of the solution does not depend on the choice of the norm.

2) Let a mapping 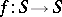be given, where 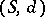is a metric space. The point 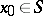is called Lyapunov stable relative to the mapping 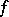if for every 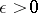there exists a 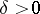such that for any 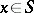satisfying the inequality , the inequality

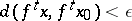holds for each 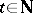. If, moreover, one can find a 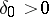such that for each 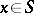satisfying 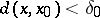one has the equation

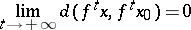(the inequality

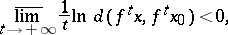respectively), then the point 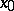is called asymptotically (respectively, exponentially) stable relative to .

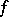Let 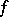be a mapping from a compact topological space 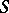into itself. A point is called Lyapunov stable (asymptotically stable) relative to 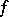if it becomes such after equipping with a metric. This property of the point does not depend on the choice of the metric.

If 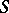is a compact differentiable manifold, then a point 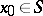is called exponentially stable relative to a mapping 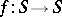if it becomes such after equipping with a certain Riemannian metric. This property of the point does not depend on the choice of the Riemannian metric.

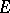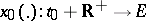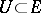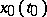3) Suppose that a differential equation (2) is given, where lies in a topological vector space . A solution of this equation is called Lyapunov stable if for each neighbourhood of zero there is a neighbourhood of in 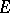such that for every 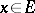the solution 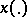of the Cauchy problem (2), 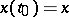, is unique, defined on 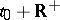and satisfies the relation 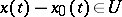for all 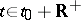. 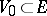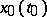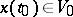If, in addition, one can find a neighbourhood of the point such that for every solution of (2) satisfying one has the equation

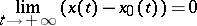(respectively,

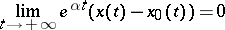for a certain 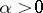), then the solution 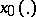is called asymptotically (respectively, exponentially) stable. If is a normed space, then this definition may be formulated as in 1 above, if as norm one takes any norm compatible with the topology on .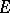

4) Let a differential equation (2) be given on a Riemannian manifold 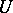(for which a Euclidean or a Hilbert space can serve as a model) or, in a more general situation, on a Finsler manifold 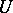(for which a normed space can serve as a model); the distance function in 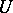is denoted by 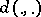. A solution 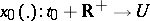of this equation is called Lyapunov stable if for each 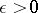one can find a 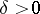such that for each 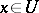satisfying 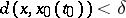, the solution 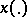of the Cauchy problem (2), 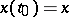, is unique, defined for 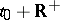and satisfies the inequality 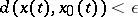for all 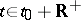. If, in addition, one can find a 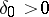such that for every solution 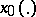of (2) whose initial value satisfies the inequality 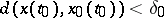one has the equation

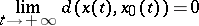(the inequality

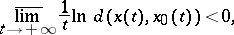respectively), then the solution 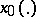is called asymptotically (respectively, exponentially) stable.

Suppose that the differential equation (2) is given on a compact differentiable manifold 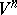. A solution of this equation is called Lyapunov stable (asymptotically, exponentially stable) if it becomes such when the manifold 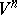is equipped with some Riemannian metric. This property of the solution does not depend on the choice of the Riemannian metric.

5) Let 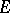be a uniform space. Let

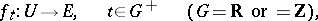be a mapping defined on an open set 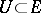. A point 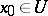is called Lyapunov stable relative to the family of mappings 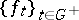if for every entourage 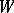there exists a neighbourhood 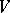of such that the set of all 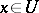satisfying 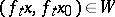for all 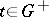, is a neighbourhood of 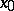. If, in addition, there exists a neighbourhood 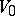of 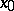such that for every 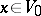and every entourage 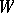one can find a 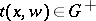such that 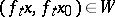for all 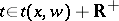, then the point 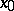is called asymptotically stable.

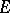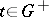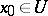If is a compact topological space and , , is a mapping given on some open set , then the point is called Lyapunov stable (asymptotically stable) relative to the family of mappings if it becomes such after the space 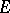is equipped with the unique uniform structure that is compatible with the topology on .

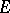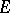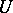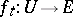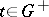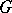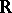6) Let be a topological space and an open subspace in it. Let , , where is or 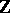, be a mapping having 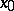as fixed point. The fixed point 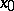is called Lyapunov stable relative to the family of mappings 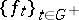if for every neighbourhood 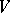of 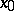there exists a neighbourhood 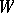of the same point such that 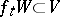for all 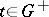. If, in addition, there exists a neighbourhood 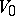of 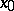such that 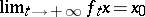for every 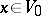, then the point 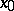is called asymptotically stable relative to the family of mappings .

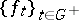7) Lyapunov stability (asymptotic, exponential stability) of a solution 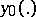of an equation of arbitrary order, , is understood to mean Lyapunov stability (respectively asymptotic, exponential stability) of the solution 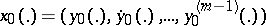of the corresponding first-order equation (2), where , .

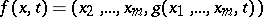Definitions 1, 2, 4, 6, 7 include stable motions of systems with a finite number of degrees of freedom (where the equations on manifolds arise naturally when considering mechanical systems with a constraint). Definitions 2–7 include stable motions in the mechanics of continuous media and in other parts of physics, stable solutions of operator equations, functional-differential equations (in particular, equations with retarded arguments) and other equations.

Study of the stability of an equilibrium position of an autonomous system.

Let 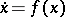be an autonomous differential equation defined in a neighbourhood of a point 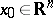, where the function 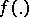is continuously differentiable and vanishes at this point. If the real parts of all eigen values of the derivative 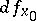are negative, then the fixed point of 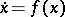is exponentially stable (Lyapunov's theorem on stability in a first approximation); to facilitate the verification of the condition in this theorem one applies criteria for stability. If under these conditions at least one of the eigen values of the derivative 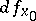has positive real part (this condition may be checked without finding the eigen values themselves, cf. Stability criterion), then the fixed point of the differential equation is unstable.

Example. The equation of the oscillation of a pendulum with friction is

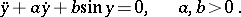The lower equilibrium position 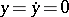is exponentially stable, since the roots of the characteristic equation 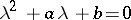of the variational equation (cf. Variational equations) have negative real parts. The upper equilibrium position 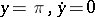is unstable, since the characteristic equation 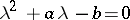of the variational equation 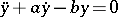has a positive root. This instability takes place even in the absence of friction 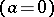. The lower equilibrium position of a pendulum without friction is one of the so-called critical cases, when all eigen values of the derivative 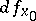are contained in the left complex half-plane, and at least one of them lies on the imaginary axis.

For the study of stability in critical cases, A.M. Lyapunov proposed the so-called second method for studying stability (cf. Lyapunov function). For a pendulum without friction,

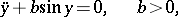the lower equilibrium position is Lyapunov stable, since there exists a Lyapunov function

— the total energy of the pendulum; the condition of non-positivity for the derivative of this function is a consequence of the law of conservation of energy.

A fixed point 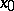of a differentiable mapping 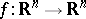is exponentially stable relative to 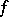if all eigen values of the derivative 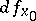are less than 1 in modulus, and it is unstable if at least one of them has modulus .

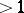The study of the stability of periodic points of differentiable mappings reduces to the study of stability of fixed points relative to the powers of these mappings. Periodic solutions of autonomous differential equations are not asymptotically stable (cf. Orbit stability; Andronov–Witt theorem).

It should not be believed that exponential stability of the null solution of the variational equation of the autonomous differential equation 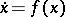along a solution 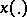implies stability of the solution. This is shown by Perron's example (cf. [2], [3]):

(3)

for the null solution of the system of variational equations,

(4)

of the system (3) (along the null solution) is exponentially stable (the Lyapunov characteristic exponents of the system (4) are 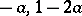, cf. Lyapunov characteristic exponent), but for the null solution of the system (3) is unstable. However, stability in the first approximation is typical, in a sense explained below.

Let 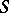be the set of diffeomorphisms of a Euclidean space onto itself having uniformly continuous derivatives that satisfy the inequality

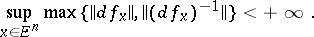For each diffeomorphism 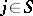denote by 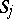the set of all 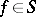satisfying the inequality

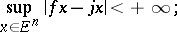one endows 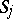with the distance function

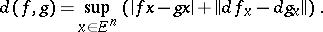For each 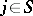there is in 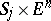an everywhere-dense set 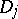of type 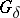with the following property: If 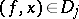is such that for every 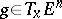the inequality

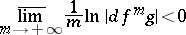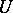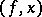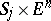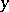holds, then there is a neighbourhood of in such that for every the point is exponentially stable relative to the diffeomorphism .

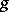For a dynamical system given on a compact differentiable manifold, an analogous theorem can be formulated more simply and as a differential-topologically invariant statement. Let 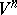be a closed differentiable manifold. The set 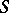of all diffeomorphisms 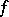of class 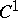mapping 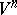to 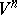can be equipped with the 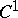-topology. In the space 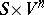there is an everywhere-dense set 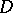of type 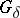with the following property: If for an the inequality

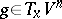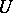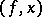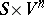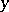holds for all , then there is a neighbourhood of in such that for each the point is exponentially stable relative to the diffeomorphism .

The concepts of Lyapunov stability, asymptotic stability and exponential stability were introduced by Lyapunov [1] in order to develop methods for studying stability in the sense of these definitions (cf. Lyapunov stability theory).

References

[1]	A.M. Lyapunov, "Stability of motion" , Acad. Press (1966) (Translated from Russian)
[2]	O. Perron, "Ueber Stabilität und asymptotisches Verhalten der Integrale von Differentialgleichungssystemen" Math. Z. , 29 (1928) pp. 129–160
[3]	R.E. Bellman, "Stability theory of differential equations" , Dover, reprint (1969)

Comments

For stability questions of differential equations with discontinuous right-hand sides cf. [a6].

References

[a1]	J.P. Lasalle, S. Lefschetz, "Stability by Lyapunov's direct method with applications" , Acad. Press (1961)
[a2]	M.W. Hirsch, S. Smale, "Differential equations, dynamical systems, and linear algebra" , Acad. Press (1974)
[a3]	W. Hahn, "Stability of motion" , Springer (1967) pp. 422
[a4]	N.P. Bhatia, G.P. Szegö, "Stability theory of dynamical systems" , Springer (1970) pp. 30–36
[a5]	M.I. Rabinovich, D.I. Trubetskov, "Oscillations and waves in linear and nonlinear systems" , Kluwer (1989) pp. Chapt. 6–7 (Translated from Russian)
[a6]	A.F. Filippov, "Differential equations with discontinuous righthand sides" , Kluwer (1989) pp. §15 (Translated from Russian)