Alternating series
From Encyclopedia of Mathematics
An infinite series whose terms are alternately positive and negative:
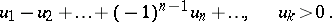 |
If the terms of an alternating series are monotone decreasing 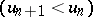 and tend to zero
and tend to zero 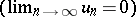 , then the series is convergent (Leibniz' theorem). The remainder term of an alternating series,
, then the series is convergent (Leibniz' theorem). The remainder term of an alternating series,
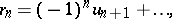 |
has the same sign as its first term and is less then the latter in absolute value. The simplest examples of alternating series are
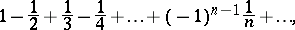 |
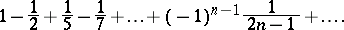 |
The sum of the first of these series is  ; that of the second is
; that of the second is 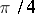 .
.
How to Cite This Entry:
Alternating series. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Alternating_series&oldid=14055
Alternating series. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Alternating_series&oldid=14055
This article was adapted from an original article by V.I. Bityutskov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article