Ring of representations

representation ring

A commutative ring 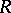defined as follows. The additive group of 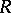is generated by the equivalence classes of linear representations of a group 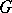over a field 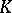, and the defining relations have the form 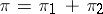, where 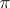is the equivalence class of a representation, 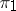is the equivalence class of a subrepresentation of it and 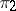is the equivalence class of the corresponding quotient representation of 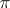; the multiplication of 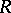assigns to two equivalence classes 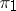and 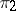the equivalence class of their tensor product. This ring of representations is sometimes called the Grothendieck ring of the group. For locally compact groups 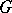the representation ring is usually meant to be the commutative ring 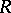defined by the operations of direct sum and tensor product in the set of equivalence classes of continuous unitary representations of . The structures of 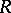are very useful if 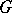is compact. Then it leads to the duality theory in terms of block-algebras. In the more general case of groups 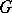of type I, the study of 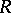may be reduced to the study of tensor products of irreducible unitary representations.

Comments

One must impose some finiteness condition on the representations under consideration, as otherwise the representation ring will be the zero ring.

A second representation ring is obtained by considering equivalence classes of suitable representations modulo split short exact sequences (instead of short exact sequences). Unless the class of representations involved consists totally of completely-reducible representations (as in the case of compact groups) the two rings of representations can be quite different.

References

[a1]	C.W. Curtis, I. Reiner, "Methods of representation theory" , II , Wiley (Interscience) (1987)