Martingale

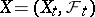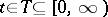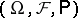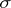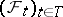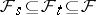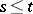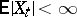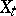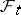A stochastic process , , defined on a probability space with a non-decreasing family of -algebras , , , such that , is -measurable and

(1)

(with probability 1). In the case of discrete time 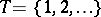; in the case of continuous time 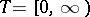. Related notions are stochastic processes which form a submartingale, if

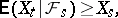or a supermartingale, if

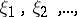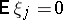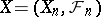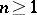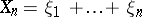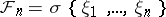Example 1. If is a sequence of independent random variables with , then , , with and the 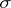-algebra generated by 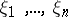, is a martingale.

Example 2. Let 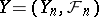be a martingale (submartingale), a predictable sequence (that is, 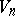is not only 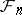-measurable but also 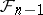-measurable, 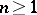), , 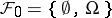and let

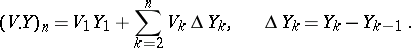Then, if the variables 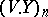are integrable, the stochastic process 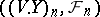forms a martingale (submartingale). In particular, if 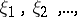is a sequence of independent random variables corresponding to a Bernoulli scheme

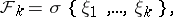and

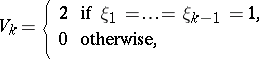(2)

then 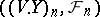is a martingale. This stochastic process is a mathematical model of a game in which a player wins one unit of capital if 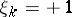and loses one unit of capital if 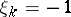, and 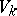is the stake at the 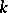-th game. The game-theoretic sense of the function 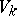defined by (2) is that the player doubles his stake when he loses and stops the game on his first win. In the gambling world such a system is called a martingale, which explains the origin of the mathematical term "martingale" .

One of the basic facts of the theory of martingales is that the structure of a martingale (submartingale) 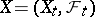is preserved under a random change of time. A precise statement of this (called the optimal sampling theorem) is the following: If 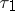and 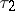are two finite stopping times (cf. Markov moment), if 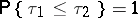and if

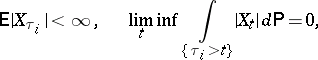(3)

then 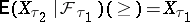(with probability 1), where

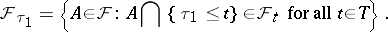As a particular case of this the Wald identity follows:

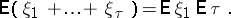Among the basic results of the theory of martingales is Doob's inequality: If 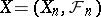is a non-negative submartingale,

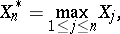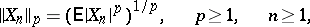then

(4)

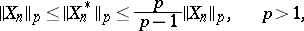(5)

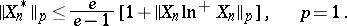(6)

If 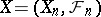is a martingale, then for 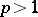the Burkholder inequalities hold (generalizations of the inequalities of Khinchin and Marcinkiewicz–Zygmund for sums of independent random variables):

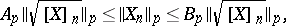(7)

where 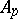and 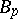are certain universal constants (not depending on 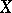or ), for which one can take

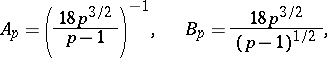and

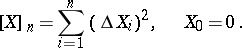Taking (5) and (7) into account, it follows that

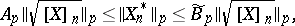(8)

where

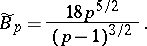When 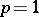inequality (8) can be generalized. Namely, Davis' inequality holds: There are universal constants 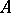and 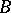such that

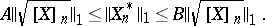In the proof of a different kind of theorem on the convergence of submartingales with probability 1, a key role is played by Doob's inequality for the mathematical expectation 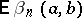of the number of upcrossings, 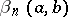, of the interval 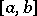by the submartingale 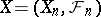in steps; namely

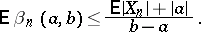(9)

The basic result on the convergence of submartingales is Doob's theorem: If 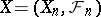is a submartingale and 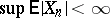, then with probability 1, 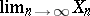(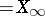) exists and 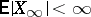. If the submartingale is uniformly integrable, then, in addition to convergence with probability 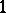, convergence in 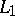holds, that is,

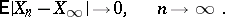A corollary of this result is Lévy's theorem on the continuity of conditional mathematical expectations: If 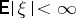, then

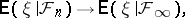where 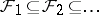and .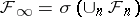

A natural generalization of a martingale is the concept of a local martingale, that is, a stochastic process 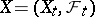for which there is a sequence 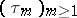of finite stopping times 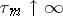(with probability 1), 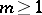, such that for each 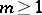the "stopped" processes

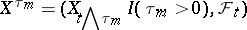are martingales. In the case of discrete time each local martingale 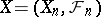is a martingale transform, that is, can be represented in the form 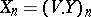, where 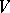is a predictable process and 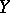is a martingale.

Each submartingale 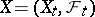has, moreover, a unique Doob–Meyer decomposition 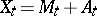, where 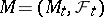is a local martingale and 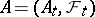is a predictable non-decreasing process. In particular, if 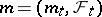is a square-integrable martingale, then its square 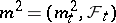is a submartingale in whose Doob–Meyer decomposition 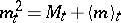the process 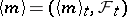is called the quadratic characteristic of the martingale . For each square-integrable martingale 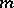and predictable process 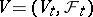such that 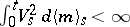(with probability 1), 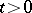, it is possible to define the stochastic integral

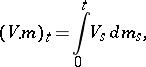which is a local martingale. In the case of a Wiener process 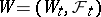, which is a square-integrable martingale, 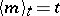and the stochastic integral 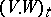is none other than the Itô stochastic integral with respect to the Wiener process.

In the case of continuous time the Doob, Burkholder and Davis inequalities are still true (for right-continuous processes having left limits).

References

[1]	J.L. Doob, "Stochastic processes" , Chapman & Hall (1953)
[2]	I.I. [I.I. Gikhman] Gihman, A.V. [A.V. Skorokhod] Skorohod, "The theory of stochastic processes" , 1 , Springer (1974) (Translated from Russian)

Comments

Stopping times are also called optimal times, or, in the older literature, Markov times or Markov moments, cf. Markov moment. The optimal sampling theorem is also called the stopping theorem or Doob's stopping theorem.

The notion of a martingale is one of the most important concepts in modern probability theory. It is basic in the theories of Markov processes and stochastic integrals, and is useful in many parts of analysis (convergence theorems in ergodic theory, derivatives and lifting in measure theory, inequalities in the theory of singular integrals, etc.). More generally one can define martingales with values in 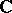, , 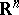a Hilbert or a Banach space; Banach-valued martingales are used in the study of Banach spaces (Radon–Nikodým property, etc.).

References

[a1]	C. Dellacherie, P.A. Meyer, "Probabilities and potential" , 1–3 , North-Holland (1978–1988) pp. Chapts. V-VIII. Theory of martingales (Translated from French)
[a2]	J.L. Doob, "Classical potential theory and its probabilistic counterpart" , Springer (1984) pp. 390
[a3]	J. Neveu, "Discrete-parameter martingales" , North-Holland (1975) (Translated from French)
[a4]	J. Ville, "Etude critique de la notion de collectif" , Gauthier-Villars (1939)
[a5]	P. Wall, C.C. Heyde, "Martingale limit theory and its application" , Acad. Press (1980)