Cyclotomic extension
of a field 
An extension  obtained from
obtained from  by adjunction of a root of unity (cf. Primitive root). The term is sometimes used for any subextension of
by adjunction of a root of unity (cf. Primitive root). The term is sometimes used for any subextension of  over
over  . An infinite algebraic extension which is the union of finite cyclotomic extensions is also called a cyclotomic extension. Important examples of cyclotomic extensions are provided by the cyclotomic fields (cf. Cyclotomic field), obtained when
. An infinite algebraic extension which is the union of finite cyclotomic extensions is also called a cyclotomic extension. Important examples of cyclotomic extensions are provided by the cyclotomic fields (cf. Cyclotomic field), obtained when 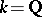 is the field of rational numbers.
is the field of rational numbers.
Let 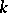 be of characteristic 0 and let
be of characteristic 0 and let  be a cyclotomic extension obtained by adjoining a primitive root of unity
be a cyclotomic extension obtained by adjoining a primitive root of unity  . Then
. Then 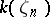 is the composite of
is the composite of  and the cyclotomic field
and the cyclotomic field 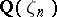 . For this reason, many properties of cyclotomic fields carry over to cyclotomic extensions. For example,
. For this reason, many properties of cyclotomic fields carry over to cyclotomic extensions. For example, 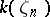 is an Abelian extension of
is an Abelian extension of 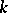 (this is also true for fields of finite characteristic), the Galois group of
(this is also true for fields of finite characteristic), the Galois group of  is a subgroup of the Galois group of
is a subgroup of the Galois group of 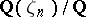 ; in particular, the order of the former Galois group divides
; in particular, the order of the former Galois group divides 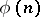 , where
, where 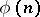 is the Euler function.
is the Euler function.
If 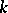 is an algebraic number field, the only prime divisors that may be ramified in
is an algebraic number field, the only prime divisors that may be ramified in 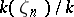 are those dividing
are those dividing  , although when
, although when 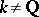 a divisor of
a divisor of  dividing
dividing  may remain unramified in
may remain unramified in 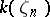 . The cyclotomic extension of an algebraic number field with Galois group
. The cyclotomic extension of an algebraic number field with Galois group 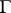 isomorphic to the additive group
isomorphic to the additive group 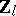 of
of 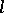 -adic numbers is called the cyclotomic
-adic numbers is called the cyclotomic  -extension (see [2], [3], [4]). In the case
-extension (see [2], [3], [4]). In the case 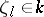 this
this 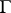 -extension has the form
-extension has the form 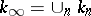 , where
, where  .
.
References
| [1] | S. Lang, "Algebra" , Addison-Wesley (1974) |
| [2] | I.R. Shafarevich, "The zeta-function" , Moscow (1969) (In Russian) |
| [3] | L.V. Kuz'min, "The Tate module of algebraic number fields" Izv. Akad. Nauk SSSR , 36 : 2 (1972) pp. 267–327 (In Russian) |
| [4] | K. Iwasawa, "On  -extensions of algebraic number fields" Ann. of Math. , 98 : 2 (1973) pp. 246–326 -extensions of algebraic number fields" Ann. of Math. , 98 : 2 (1973) pp. 246–326 |
Cyclotomic extension. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Cyclotomic_extension&oldid=14022