Dispersion ellipsoid

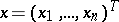An ellipsoid in the realization space of a random vector describing the concentration of its probability distribution around a certain prescribed vector in terms of the second-order moments. Let be a random vector assuming values in the -dimensional Euclidean space 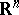and having non-singular covariance matrix 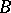. Then, for any fixed vector in the realization space 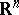, one can define an ellipsoid

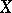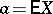called a dispersion ellipsoid of the probability distribution of with respect to , or a dispersion ellipsoid of the random vector . In particular, if , then the dispersion ellipsoid is a geometric characteristic of the concentration of the probability distribution of 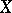around its mathematical expectation .

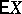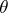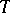In the problem of the statistical estimation of an unknown -dimensional parameter , the concept of a dispersion ellipsoid can be used to define a partial order on the set of all unbiased estimators of 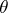having non-singular covariance matrices, in the following way: Given two estimators , the preferred one is 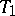if the dispersion ellipsoid of 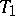lies wholly inside that of 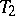. These unbiased efficient estimators of an unknown vector parameter are optimal in the sense that the dispersion ellipsoid of such an unbiased efficient estimator lies inside that of any other unbiased estimator. See Rao–Cramér inequality; Efficient estimator; Information, amount of.

References

[1]	H. Cramér, M.R. Leadbetter, "Stationary and related stochastic processes" , Wiley (1967)
[2]	T.W. Anderson, "An introduction to multivariate statistical analysis" , Wiley (1958)
[3]	I.S. Ibragimov, "Statistical estimation: asymptotic theory" , Springer (1981) (Translated from Russian)