Meromorphic mapping
of complex spaces
A generalization of the notion of a meromorphic function. Let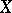 
and 
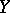be complex spaces (cf. Complex space), let 
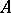be an open subset of 
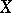such that 
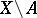is a nowhere-dense analytic subset (cf. Analytic set) and suppose that an analytic mapping 
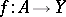has been given. Then 
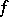is called a meromorphic mapping of 
into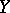 
if the closure 
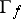of the graph 
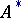of 
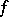in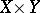 
is an analytic subset of 
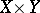and if the projection 
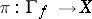is a proper mapping (cf. also Proper morphism). The set 
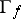is called the graph of the meromorphic mapping 
. The mapping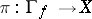 
is surjective and defines a bijective mapping of the set of irreducible components. If 
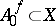denotes the largest open subset to which 
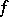can be extended as an analytic mapping, then 
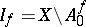is a nowhere-dense analytic subset of 
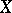, called the set of indeterminacy of 
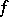. The set 
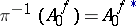is open and dense in 
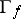; also, 
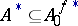and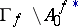 
is analytic and nowhere dense in 
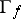. The restriction 
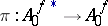is an isomorphism of analytic spaces. If 
is a normal complex space (cf. Normal analytic space), then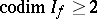 
and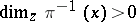 
if and only if 
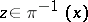and 
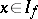. If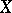 
is not normal, 
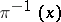may consist of a finite number of points, even if 
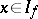. In the case 
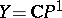the notion of a meromorphic mapping reduces to that of a meromorphic function.
Let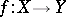 
, 
, 
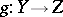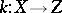be meromorphic mappings of complex spaces. One says that the composite 
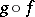of the mappings 
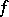and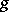 
is defined and equals 
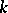if there is an open dense subset 
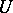of 
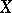such that 
, 
, 
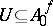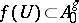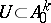, and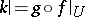 
. A meromorphic mapping 
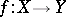is called bimeromorphic if there is a meromorphic mapping 
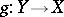such that 
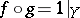and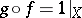 
. Composition of two bimeromorphic mappings 
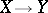and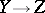 
is always defined.
References
| [1] | A. Andreotti, W. Stoll, "Analytic and algebraic dependence of meromorphic functions" , Springer (1971) |
| [2] | R. Remmert, "Holomorphe und meromorphe Abbildungen komplexer Räume" Math. Ann. , 133 : 3 (1957) pp. 328–370 |
Comments
References
| [a1] | H. Whitney, "Complex analytic varieties" , Addison-Wesley (1972) pp. Sect. 6.3 |
Meromorphic mapping. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Meromorphic_mapping&oldid=13951