Homology functor
A functor on an Abelian category that defines a certain homological structure on it. A system 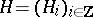 of covariant additive functors from an Abelian category
of covariant additive functors from an Abelian category 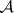 into an Abelian category
into an Abelian category  is called a homology functor if the following axioms are satisfied.
is called a homology functor if the following axioms are satisfied.
1) For each exact sequence
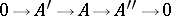 |
and each 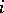 , in
, in  a morphism
a morphism  is given, which is known as the connecting or boundary morphism.
is given, which is known as the connecting or boundary morphism.
2) The sequence
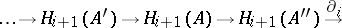 |
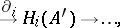 |
called the homology sequence, is exact.
Thus, let 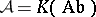 be the category of chain complexes of Abelian groups, and let
be the category of chain complexes of Abelian groups, and let 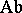 be the category of Abelian groups. The functors
be the category of Abelian groups. The functors 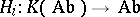 which assign to a complex
which assign to a complex 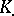 the corresponding homology groups
the corresponding homology groups 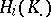 define a homology functor.
define a homology functor.
Let 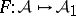 be an additive covariant functor for which the left derived functors
be an additive covariant functor for which the left derived functors 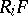 (
( ,
, 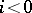 ) are defined (cf. Derived functor). The system
) are defined (cf. Derived functor). The system 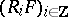 will then define a homology functor from
will then define a homology functor from 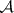 into
into 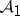 .
.
Another example of a homology functor is the hyperhomology functor.
A cohomology functor is defined in a dual manner.
References
| [1] | A. Grothendieck, "Sur quelques points d'algèbre homologique" Tohoku Math. J. , 9 (1957) pp. 119–221 |
Homology functor. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Homology_functor&oldid=13881