Weber function, Weber–Hermite function
A solution of the differential equation
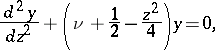 | (*) |
which is obtained as a result of separating the variables in the wave equation 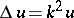 in parabolic cylindrical coordinates (cf. Parabolic coordinates). Ordinarily one uses the solution
in parabolic cylindrical coordinates (cf. Parabolic coordinates). Ordinarily one uses the solution
where 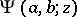 is the confluent hypergeometric function. The functions
is the confluent hypergeometric function. The functions 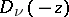 and
and 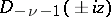 also satisfy equation (*). The functions
also satisfy equation (*). The functions 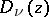 and
and 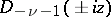 are linearly independent for arbitrary
are linearly independent for arbitrary  , and
, and 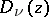 and
and 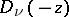 are linearly independent for
are linearly independent for 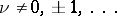 . The parabolic cylinder functions are entire functions of
. The parabolic cylinder functions are entire functions of  . The function
. The function 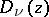 is real for real
is real for real  and
and  .
.
The differentiation formulas are, 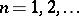 :
:
The recurrence formulas are:
Asymptotically, for fixed  and
and  , as
, as 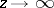 , one has
, one has
and, for bounded 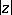 and
and 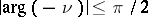 , as
, as 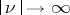 , one has
, one has
Parabolic cylinder functions are related to other functions as follows (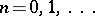 ): To the Hermite polynomials by
): To the Hermite polynomials by
to the probability integral (error function) by
and to the Bessel functions by
References
| [1] | H. Bateman (ed.) A. Erdélyi (ed.) et al. (ed.) , Higher transcendental functions , 2. Bessel functions, parabolic cylinder functions, orthogonal polynomials , McGraw-Hill (1953) |
| [2] | J.C.P. Miller, "Giving solutions of the differential equation 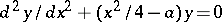 , tables of Weber parabolic cylinder functions" , H.M. Stationary Office (1955) , tables of Weber parabolic cylinder functions" , H.M. Stationary Office (1955) |
How to Cite This Entry:
Parabolic cylinder function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Parabolic_cylinder_function&oldid=13870
This article was adapted from an original article by Yu.A. BrychkovA.P. Prudnikov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098.
See original article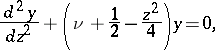
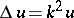 in parabolic cylindrical coordinates (cf. Parabolic coordinates). Ordinarily one uses the solution
in parabolic cylindrical coordinates (cf. Parabolic coordinates). Ordinarily one uses the solution
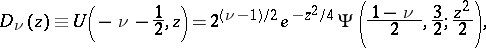
 is the confluent hypergeometric function. The functions
is the confluent hypergeometric function. The functions 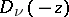 and
and 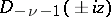 also satisfy equation (*). The functions
also satisfy equation (*). The functions 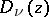 and
and 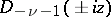 are linearly independent for arbitrary
are linearly independent for arbitrary  , and
, and 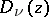 and
and 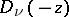 are linearly independent for
are linearly independent for 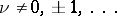 . The parabolic cylinder functions are entire functions of
. The parabolic cylinder functions are entire functions of  . The function
. The function 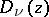 is real for real
is real for real  and
and  .
.
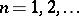 :
:
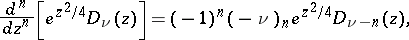
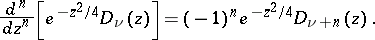
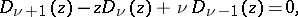
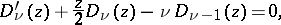
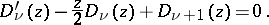
 and
and  , as
, as 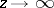 , one has
, one has
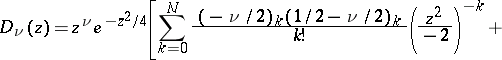
 and
and 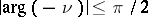 , as
, as 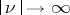 , one has
, one has
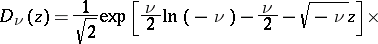
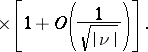
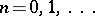 ): To the Hermite polynomials by
): To the Hermite polynomials by
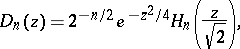
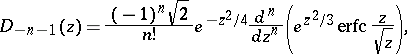
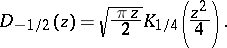
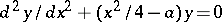 , tables of Weber parabolic cylinder functions" , H.M. Stationary Office (1955)
, tables of Weber parabolic cylinder functions" , H.M. Stationary Office (1955)