Lebesgue function
From Encyclopedia of Mathematics
A function
 |
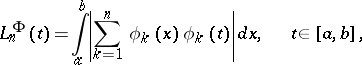where 
is a given system of functions, orthonormal with respect to the Lebesgue measure on the interval 
, 
. Lebesgue functions are defined similarly in the case when an orthonormal system is specified on an arbitrary measure space. One has
 |
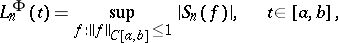where
 |
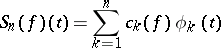is the 
-th partial sum of the Fourier series of 
with respect to 
. In the case when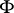 
is the trigonometric system, the Lebesgue functions are constant and reduce to the Lebesgue constants. They were introduced by H. Lebesgue.
References
| [1] | S. Kaczmarz, H. Steinhaus, "Theorie der Orthogonalreihen" , Chelsea, reprint (1951) |
How to Cite This Entry:
Lebesgue function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Lebesgue_function&oldid=13866
Lebesgue function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Lebesgue_function&oldid=13866
This article was adapted from an original article by B.S. Kashin (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article