Commuting operators
Linear operators 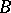 and
and 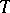 , of which
, of which 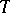 is of general type and
is of general type and 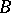 is bounded, and which are such that
is bounded, and which are such that
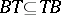 | (1) |
(the symbol 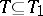 means that
means that 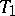 is an extension of
is an extension of 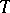 , cf. Extension of an operator). The commutation relation is denoted by
, cf. Extension of an operator). The commutation relation is denoted by 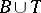 and satisfies the following rules:
and satisfies the following rules:
1) if 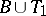 ,
, 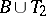 , then
, then 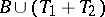 ,
, 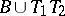 ;
;
2) if 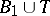 ,
, 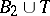 , then
, then  ,
, 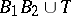 ;
;
3) if 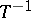 exists, then
exists, then 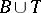 implies that
implies that 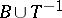 ;
;
4) if 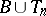 ,
, 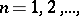 then
then 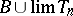 ;
;
5) if 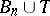 ,
, 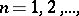 then
then 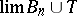 , provided that
, provided that 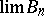 is bounded and
is bounded and 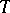 is closed.
is closed.
If the two operators are defined on the entire space, condition 1) reduces to the usual one:
 | (2) |
and 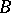 is not required to be bounded. The generalization of (2) is justified by the fact that even a bounded operator
is not required to be bounded. The generalization of (2) is justified by the fact that even a bounded operator 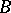 need not commute with its inverse
need not commute with its inverse 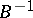 if the latter is not defined on the entire space.
if the latter is not defined on the entire space.
References
| [1] | L.A. Lyusternik, V.I. Sobolev, "Elements of functional analysis" , Hindushtan Publ. Comp. (1974) (Translated from Russian) |
| [2] | F. Riesz, B. Szökefalvi-Nagy, "Functional analysis" , F. Ungar (1955) (Translated from French) |
Commuting operators. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Commuting_operators&oldid=13863