Lie algebroid
Lie algebroids were first introduced and studied by J. Pradines [a11], following work by Ch. Ehresmann and P. Libermann on differentiable groupoids (later called Lie groupoids). Just as Lie algebras are the infinitesimal objects of Lie groups, Lie algebroids are the infinitesimal objects of Lie groupoids (cf. also Lie group). They are generalizations of both Lie algebras and tangent vector bundles (cf. also Lie algebra; Vector bundle; Tangent bundle). For a comprehensive treatment and lists of references, see [a8], [a9]. See also [a1], [a4], [a6], [a13], [a14].
A real Lie algebroid 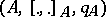 is a smooth real vector bundle
is a smooth real vector bundle 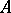 over a base
over a base 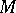 , with a real Lie algebra structure
, with a real Lie algebra structure 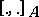 on the vector space
on the vector space 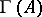 of smooth global sections of
of smooth global sections of  , and a morphism of vector bundles
, and a morphism of vector bundles 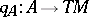 , where
, where 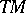 is the tangent bundle of
is the tangent bundle of  , called the anchor, such that
, called the anchor, such that
 , for all
, for all 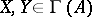 and
and 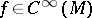 ;
;
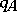 defines a Lie algebra homomorphism from the Lie algebra of sections of
defines a Lie algebra homomorphism from the Lie algebra of sections of 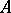 , with Lie bracket
, with Lie bracket 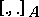 , into the Lie algebra of vector fields on
, into the Lie algebra of vector fields on 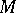 . Complex Lie algebroid structures [a1] on complex vector bundles over real bases can be defined similarly, replacing the tangent bundle of the base by the complexified tangent bundle.
. Complex Lie algebroid structures [a1] on complex vector bundles over real bases can be defined similarly, replacing the tangent bundle of the base by the complexified tangent bundle.
The space of sections of a Lie algebroid is a Lie–Rinehart algebra, also called a Lie 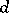 -ring or a Lie pseudo-algebra. (See [a4], [a6], [a9].) More precisely, it is a
-ring or a Lie pseudo-algebra. (See [a4], [a6], [a9].) More precisely, it is a 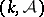 -Lie algebra, where
-Lie algebra, where 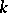 is the field of real (or complex) numbers and
is the field of real (or complex) numbers and  is the algebra of functions on the base manifold. In fact, the Lie–Rinehart algebras are the algebraic counterparts of the Lie algebroids, just as the modules over a ring are the algebraic counterparts of the vector bundles.
is the algebra of functions on the base manifold. In fact, the Lie–Rinehart algebras are the algebraic counterparts of the Lie algebroids, just as the modules over a ring are the algebraic counterparts of the vector bundles.
Examples.
1) A Lie algebroid over a one-point set, with the zero anchor, is a Lie algebra.
2) The tangent bundle 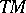 of a manifold
of a manifold 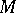 , with as bracket the Lie bracket of vector fields and with as anchor the identity of
, with as bracket the Lie bracket of vector fields and with as anchor the identity of 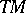 , is a Lie algebroid over
, is a Lie algebroid over 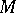 . Any integrable sub-bundle of
. Any integrable sub-bundle of  , in particular the tangent bundle along the leaves of a foliation, is also a Lie algebroid.
, in particular the tangent bundle along the leaves of a foliation, is also a Lie algebroid.
3) A vector bundle with a smoothly varying Lie algebra structure on the fibres (in particular, a Lie-algebra bundle [a8]) is a Lie algebroid, with pointwise bracket of sections and zero anchor.
4) If 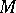 is a Poisson manifold, then the cotangent bundle
is a Poisson manifold, then the cotangent bundle 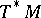 of
of 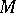 is, in a natural way, a Lie algebroid over
is, in a natural way, a Lie algebroid over 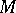 . The anchor is the mapping
. The anchor is the mapping 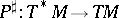 defined by the Poisson bivector
defined by the Poisson bivector 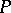 . The Lie bracket
. The Lie bracket 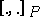 of differential
of differential  -forms satisfies
-forms satisfies 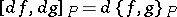 , for any functions
, for any functions 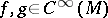 , where
, where 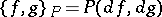 is the Poisson bracket (cf. Poisson brackets) of functions, defined by
is the Poisson bracket (cf. Poisson brackets) of functions, defined by 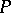 . When
. When  is non-degenerate,
is non-degenerate, 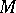 is a symplectic manifold (cf. also Symplectic structure) and this Lie algebra structure of
is a symplectic manifold (cf. also Symplectic structure) and this Lie algebra structure of 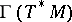 is isomorphic to that of
is isomorphic to that of 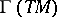 . For references to the early occurrences of this bracket, which seems to have first appeared in [a3], see [a4], [a6] and [a13]. It was shown in [a2] that
. For references to the early occurrences of this bracket, which seems to have first appeared in [a3], see [a4], [a6] and [a13]. It was shown in [a2] that 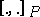 is a Lie algebroid bracket on
is a Lie algebroid bracket on 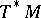 .
.
5) The Lie algebroid of a Lie groupoid 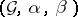 , where
, where  is the source mapping and
is the source mapping and 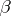 is the target mapping [a11], [a8], [a13]. It is defined as the normal bundle along the base of the groupoid, whose sections can be identified with the right-invariant,
is the target mapping [a11], [a8], [a13]. It is defined as the normal bundle along the base of the groupoid, whose sections can be identified with the right-invariant,  -vertical vector fields. The bracket is induced by the Lie bracket of vector fields on the groupoid, and the anchor is
-vertical vector fields. The bracket is induced by the Lie bracket of vector fields on the groupoid, and the anchor is 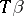 .
.
6) The Atiyah sequence. If  is a principal bundle with structure group
is a principal bundle with structure group 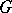 , base
, base 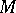 and projection
and projection 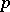 , the
, the  -invariant vector fields on
-invariant vector fields on 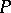 are the sections of a vector bundle with base
are the sections of a vector bundle with base 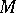 , denoted by
, denoted by 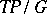 , and sometimes called the Atiyah bundle of the principal bundle
, and sometimes called the Atiyah bundle of the principal bundle 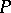 . This vector bundle is a Lie algebroid, with bracket induced by the Lie bracket of vector fields on
. This vector bundle is a Lie algebroid, with bracket induced by the Lie bracket of vector fields on 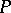 , and with surjective anchor induced by
, and with surjective anchor induced by 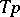 . The kernel of the anchor is the adjoint bundle,
. The kernel of the anchor is the adjoint bundle, 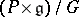 . Splittings of the anchor are connections on
. Splittings of the anchor are connections on 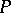 (cf. also Connection). The Atiyah bundle of
(cf. also Connection). The Atiyah bundle of 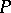 is the Lie algebroid of the Ehresmann gauge groupoid
is the Lie algebroid of the Ehresmann gauge groupoid 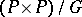 . If
. If 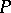 is the frame bundle of a vector bundle
is the frame bundle of a vector bundle 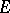 , then the sections of the Atiyah bundle of
, then the sections of the Atiyah bundle of 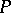 are the covariant differential operators on
are the covariant differential operators on  , in the sense of [a8].
, in the sense of [a8].
7) Other examples are: the trivial Lie algebroids 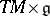 ; the transformation Lie algebroids
; the transformation Lie algebroids  , where the Lie algebra
, where the Lie algebra 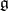 acts on the manifold
acts on the manifold 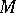 ; the deformation Lie algebroid
; the deformation Lie algebroid  of a Lie algebroid
of a Lie algebroid 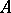 , where
, where 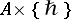 , for
, for 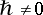 , is isomorphic to
, is isomorphic to 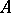 , and
, and 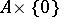 is isomorphic to the vector bundle
is isomorphic to the vector bundle 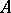 with the Abelian Lie algebroid structure (zero bracket and zero anchor); the prolongation Lie algebroids of a Lie algebroid, etc.
with the Abelian Lie algebroid structure (zero bracket and zero anchor); the prolongation Lie algebroids of a Lie algebroid, etc.
de Rham differential.
Given any Lie algebroid 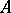 , a differential
, a differential 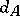 is defined on the graded algebra of sections of the exterior algebra of the dual vector bundle,
is defined on the graded algebra of sections of the exterior algebra of the dual vector bundle, 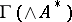 , called the de Rham differential of
, called the de Rham differential of 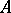 . Then
. Then 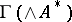 can be considered as the algebra of functions on a super-manifold,
can be considered as the algebra of functions on a super-manifold, 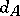 being an odd vector field with square zero [a12].
being an odd vector field with square zero [a12].
If  is a Lie algebra
is a Lie algebra 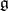 , then
, then  is the Chevalley–Eilenberg cohomology operator on
is the Chevalley–Eilenberg cohomology operator on 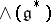 .
.
If 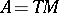 , then
, then  is the usual de Rham differential on forms.
is the usual de Rham differential on forms.
If 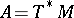 is the cotangent bundle of a Poisson manifold, then
is the cotangent bundle of a Poisson manifold, then 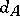 is the Lichnerowicz–Poisson differential
is the Lichnerowicz–Poisson differential 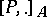 on fields of multi-vectors on
on fields of multi-vectors on 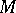 .
.
Schouten algebra.
Given any Lie algebroid  , there is a Gerstenhaber algebra structure (see Poisson algebra), denoted by
, there is a Gerstenhaber algebra structure (see Poisson algebra), denoted by 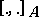 , on the graded algebra of sections of the exterior algebra of the vector bundle
, on the graded algebra of sections of the exterior algebra of the vector bundle 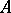 ,
, 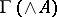 . With this graded Lie bracket,
. With this graded Lie bracket,  is called the Schouten algebra of
is called the Schouten algebra of 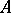 .
.
If 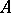 is a Lie algebra
is a Lie algebra  , then
, then 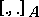 is the algebraic Schouten bracket on
is the algebraic Schouten bracket on 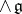 .
.
If 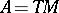 , then
, then 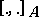 is the usual Schouten bracket of fields of multi-vectors on
is the usual Schouten bracket of fields of multi-vectors on 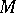 .
.
If  is the cotangent bundle of a Poisson manifold, then
is the cotangent bundle of a Poisson manifold, then 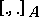 is the Koszul bracket [a7], [a13], [a5] of differential forms.
is the Koszul bracket [a7], [a13], [a5] of differential forms.
Morphisms of Lie algebroids and the linear Poisson structure on the dual.
A base-preserving morphism from a Lie algebroid 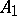 to a Lie algebroid
to a Lie algebroid  , over the same base
, over the same base 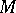 , is a base-preserving vector-bundle morphism,
, is a base-preserving vector-bundle morphism, 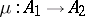 , such that
, such that 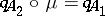 , inducing a Lie-algebra morphism from
, inducing a Lie-algebra morphism from 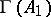 to
to 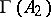 .
.
If 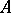 is a Lie algebroid, the dual vector bundle
is a Lie algebroid, the dual vector bundle 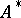 is a Poisson vector bundle. This means that the total space of
is a Poisson vector bundle. This means that the total space of 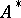 has a Poisson structure such that the Poisson brackets of two functions which are linear on the fibres is linear on the fibres. A base-preserving morphism from a vector bundle
has a Poisson structure such that the Poisson brackets of two functions which are linear on the fibres is linear on the fibres. A base-preserving morphism from a vector bundle 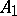 to a vector bundle
to a vector bundle 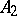 is a morphism of Lie algebroids if and only if its transpose is a Poisson morphism.
is a morphism of Lie algebroids if and only if its transpose is a Poisson morphism.
Lie bi-algebroids.
These are pairs of Lie algebroids 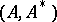 in duality satisfying the compatibility condition that
in duality satisfying the compatibility condition that 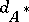 be a derivation of the graded Lie bracket
be a derivation of the graded Lie bracket 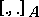 [a10], [a5]. They generalize the Lie bi-algebras in the sense of V.G. Drinfel'd (see Quantum groups and Poisson Lie group) and also the pair
[a10], [a5]. They generalize the Lie bi-algebras in the sense of V.G. Drinfel'd (see Quantum groups and Poisson Lie group) and also the pair 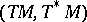 , where
, where 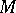 is a Poisson manifold.
is a Poisson manifold.
There is no analogue to Lie's third theorem (cf. also Lie theorem) in the case of Lie algebroids, since not every Lie algebroid can be integrated to a global Lie groupoid, although there are local versions of this result. (See [a8], [a1].)
References
| [a1] | A. Cannas da Silva, A. Weinstein, "Geometric models for noncommutative algebras" , Berkeley Math. Lecture Notes , 10 , Amer. Math. Soc. (1999) |
| [a2] | A. Coste, P. Dazord, A. Weinstein, "Groupoïdes symplectiques" Publ. Dép. Math. Univ. Claude Bernard, Lyon I , 2A (1987) pp. 1–62 |
| [a3] | B. Fuchssteiner, "The Lie algebra structure of degenerate Hamiltonian and bi-Hamiltonian systems" Prog. Theor. Phys. , 68 (1982) pp. 1082–1104 |
| [a4] | J. Huebschmann, "Poisson cohomology and quantization" J. Reine Angew. Math. , 408 (1990) pp. 57–113 |
| [a5] | Y. Kosmann-Schwarzbach, "Exact Gerstenhaber algebras and Lie bialgebroids" Acta Applic. Math. , 41 (1995) pp. 153–165 |
| [a6] | Y. Kosmann-Schwarzbach, F. Magri, "Poisson–Nijenhuis structures" Ann. Inst. H. Poincaré Phys. Theor. , 53 (1990) pp. 35–81 |
| [a7] | J.-L. Koszul, "Crochet de Schouten–Nijenhuis et cohomologie" Astérisque, Hors Sér. (1985) pp. 257–271 |
| [a8] | K. Mackenzie, "Lie groupoids and Lie algebroids in differential geometry" , Cambridge Univ. Press (1987) |
| [a9] | K. Mackenzie, "Lie algebroids and Lie pseudoalgebras" Bull. London Math. Soc. , 27 (1995) pp. 97–147 |
| [a10] | K. Mackenzie, P. Xu, "Lie bialgebroids and Poisson groupoids" Duke Math. J. , 73 (1994) pp. 415–452 |
| [a11] | J. Pradines, "Théorie de Lie pour les groupoïdes différentiables. Calcul différentiel dans la catégorie des groupoïdes infinitésimaux" C.R. Acad. Sci. Paris , 264 A (1967) pp. 245–248 |
| [a12] | A. Vaintrob, "Lie algebroids and homological vector fields" Russian Math. Surveys , 52 (1997) pp. 428–429 |
| [a13] | I. Vaisman, "Lectures on the geometry of Poisson manifolds" , Birkhäuser (1994) |
| [a14] | A. Weinstein, "Poisson geometry" Diff. Geom. Appl. , 9 (1998) pp. 213–238 |
Lie algebroid. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Lie_algebroid&oldid=13860