Half-martingale
From Encyclopedia of Mathematics
A concept equivalent to either the concept of a submartingale or that of a supermartingale. A stochastic sequence 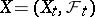 ,
, 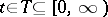 , defined on a probability space
, defined on a probability space 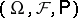 with a distinguished non-decreasing family of
with a distinguished non-decreasing family of 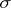 -algebras
-algebras 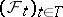 ,
,  ,
, 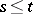 , is called a half-martingale if
, is called a half-martingale if 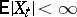 ,
,  is
is 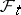 -measurable and with probability 1 either
-measurable and with probability 1 either
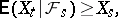 | (1) |
or
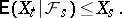 | (2) |
In case (1) the sequence is called a submartingale, and in case (2) — a supermartingale.
In the modern literature, the term "half-martingale" is either not used at all or identified with the concept of a submartingale (supermartingales are derived from submartingales by a change of sign and are sometimes called lower half-martingales). See also Martingale.
How to Cite This Entry:
Half-martingale. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Half-martingale&oldid=13853
Half-martingale. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Half-martingale&oldid=13853
This article was adapted from an original article by A.V. Prokhorov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article