Central simple algebra
A simple associative algebra with a unit element that is a central algebra. Every finite-dimensional central simple algebra 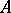 over a field
over a field 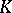 is isomorphic to a matrix algebra
is isomorphic to a matrix algebra 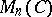 over a finite-dimensional central division algebra
over a finite-dimensional central division algebra 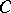 over
over 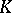 . In particular, if
. In particular, if 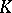 is algebraically closed, then every finite-dimensional central simple algebra
is algebraically closed, then every finite-dimensional central simple algebra 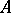 over
over 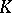 is isomorphic to
is isomorphic to 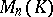 , and if
, and if 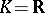 , then
, then 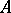 is isomorphic to the algebra of real or quaternion matrices. The tensor product of a central simple algebra
is isomorphic to the algebra of real or quaternion matrices. The tensor product of a central simple algebra 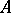 and an arbitrary simple algebra
and an arbitrary simple algebra 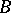 is a simple algebra, which is central if
is a simple algebra, which is central if 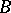 is central. Two finite-dimensional central simple algebras
is central. Two finite-dimensional central simple algebras 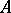 and
and 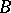 over
over 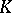 are called equivalent if
are called equivalent if
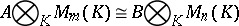 |
for certain 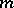 and
and  , or, which is equivalent, if
, or, which is equivalent, if 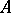 and
and 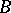 are isomorphic matrix algebras over one and the same central division algebra. The equivalence classes of central simple algebras over
are isomorphic matrix algebras over one and the same central division algebra. The equivalence classes of central simple algebras over 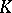 form the Brauer group of
form the Brauer group of 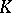 relative to the operation induced by tensor multiplication.
relative to the operation induced by tensor multiplication.
References
| [1] | B.L. van der Waerden, "Algebra" , 1–2 , Springer (1967–1971) (Translated from German) |
| [2] | Yu.A. Drozd, V.V. Kirichenko, "Finite-dimensional algebras" , Kiev (1980) (In Russian) |
Comments
References
| [a1] | R.S. Peirce, "Associative algebras" , Springer (1980) |
| [a2] | A.A. Albert, "Structure of algebras" , Amer. Math. Soc. (1939) |
| [a3] | M. Deuring, "Algebren" , Springer (1935) |
| [a4] | I.N. Herstein, "Noncommutative rings" , Math. Assoc. Amer. (1968) |
| [a5] | N. Jacobson, "Structure of rings" , Amer. Math. Soc. (1956) |
Central simple algebra. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Central_simple_algebra&oldid=13839