Singular function
A non-constant continuous function of bounded variation whose derivative is zero almost-everywhere on the interval on which it is defined. Singular functions arise as summands in the Lebesgue decomposition of functions of bounded variation. For example, every continuous function 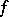 of bounded variation on an interval
of bounded variation on an interval 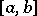 can be uniquely written in the form of a sum
can be uniquely written in the form of a sum 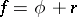 , where
, where 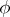 is an absolutely-continuous function (cf. Absolute continuity) with
is an absolutely-continuous function (cf. Absolute continuity) with 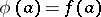 and
and  is a singular function or identically zero.
is a singular function or identically zero.
Example. Let 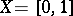 . Any
. Any 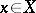 can be written in the form
can be written in the form
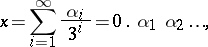 |
where 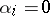 ,
, 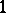 or 2 for
or 2 for 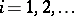 . Thus, if
. Thus, if 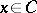 , where
, where  is the Cantor set, then
is the Cantor set, then 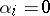 or 2 for all
or 2 for all 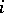 . Let
. Let 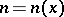 be the first subscript for which
be the first subscript for which 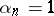 ; if there are no such subscripts, then one takes
; if there are no such subscripts, then one takes 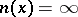 . The function
. The function
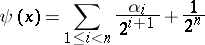 |
is then a monotone singular function on 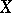 .
.
References
| [1] | H. Lebesgue, "Leçons sur l'intégration et la récherche des fonctions primitives" , Gauthier-Villars (1928) |
| [2] | I.P. Natanson, "Theory of functions of a real variable" , 1–2 , F. Ungar (1955–1961) (Translated from Russian) |
| [3] | P.R. Halmos, "Measure theory" , v. Nostrand (1950) |
Comments
The function 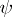 is well-defined (i.e. the value
is well-defined (i.e. the value 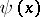 does not depend on the chosen representation of
does not depend on the chosen representation of  ); it is known as Lebesgue's singular function.
); it is known as Lebesgue's singular function.
References
| [a1] | E. Hewitt, K.R. Stromberg, "Real and abstract analysis" , Springer (1965) |
| [a2] | K.R. Stromberg, "Introduction to classical real analysis" , Wadsworth (1981) |
Singular function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Singular_function&oldid=13838