Random function
A function of an arbitrary argument 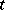 (defined on the set
(defined on the set 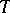 of its values, and taking numerical values or, more generally, values in a vector space) whose values are defined in terms of a certain experiment and may vary with the outcome of this experiment according to a given probability distribution. In probability theory, attention centres on numerical (that is, scalar) random functions
of its values, and taking numerical values or, more generally, values in a vector space) whose values are defined in terms of a certain experiment and may vary with the outcome of this experiment according to a given probability distribution. In probability theory, attention centres on numerical (that is, scalar) random functions 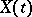 ; a random vector function
; a random vector function 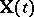 can be regarded as the aggregate of the scalar functions
can be regarded as the aggregate of the scalar functions 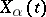 , where
, where 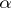 ranges over the finite or countable set
ranges over the finite or countable set  of components of
of components of  , that is, as a numerical random function on the set
, that is, as a numerical random function on the set  of pairs
of pairs 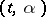 ,
, 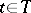 ,
, 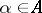 .
.
When 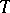 is finite,
is finite, 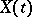 is a finite set of random variables, and can be regarded as a multi-dimensional (vector) random variable characterized by a multi-dimensional distribution function. When
is a finite set of random variables, and can be regarded as a multi-dimensional (vector) random variable characterized by a multi-dimensional distribution function. When 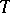 is infinite, the case mostly studied is that in which
is infinite, the case mostly studied is that in which 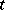 takes numerical (real) values; in this case,
takes numerical (real) values; in this case, 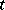 usually denotes time, and
usually denotes time, and 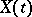 is called a stochastic process, or, if
is called a stochastic process, or, if 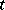 takes only integral values, a random sequence (or time series). If the values of
takes only integral values, a random sequence (or time series). If the values of 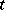 are the points of a manifold (such as a
are the points of a manifold (such as a 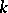 -dimensional Euclidean space
-dimensional Euclidean space 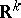 ), then
), then 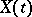 is called a random field.
is called a random field.
The probability distribution of the values of a random function 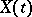 defined on an infinite set
defined on an infinite set 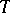 is characterized by the aggregate of finite-dimensional probability distributions of sets of random variables
is characterized by the aggregate of finite-dimensional probability distributions of sets of random variables 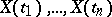 corresponding to all finite subsets
corresponding to all finite subsets 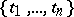 of
of 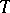 , that is, the aggregate of corresponding finite-dimensional distribution functions
, that is, the aggregate of corresponding finite-dimensional distribution functions 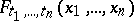 , satisfying the consistency conditions:
, satisfying the consistency conditions:
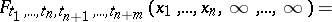 | (1) |
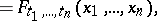 |
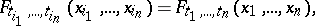 | (2) |
where  is an arbitrary permutation of the subscripts
is an arbitrary permutation of the subscripts 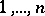 . This characterization of the probability distribution of
. This characterization of the probability distribution of  is sufficient in all cases when one is only interested in events depending on the values of
is sufficient in all cases when one is only interested in events depending on the values of 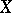 on countable subsets of
on countable subsets of 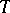 . But it does not enable one to determine the probability of properties of
. But it does not enable one to determine the probability of properties of 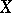 that depend on its values on a continuous subset of
that depend on its values on a continuous subset of 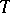 , such as the probability of continuity or differentiability, or the probability that
, such as the probability of continuity or differentiability, or the probability that 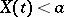 on a continuous subset of
on a continuous subset of 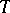 (see Separable process).
(see Separable process).
Random functions can be described more generally in terms of aggregates of random variables 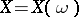 defined on a fixed probability space
defined on a fixed probability space 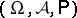 (where
(where  is a set of points
is a set of points 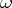 ,
, 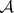 is a
is a 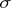 -algebra of subsets of
-algebra of subsets of  and
and 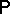 is a given probability measure on
is a given probability measure on  ), one for each point
), one for each point 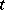 of
of 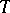 . In this approach, a random function on
. In this approach, a random function on 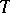 is regarded as a function
is regarded as a function 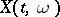 of two variables
of two variables 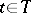 and
and 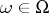 which is
which is 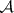 -measurable for every
-measurable for every 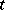 (that is, for fixed
(that is, for fixed 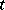 it reduces to a random variable defined on the probability space
it reduces to a random variable defined on the probability space  ). By taking a fixed value
). By taking a fixed value 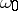 of
of 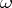 , one obtains a numerical function
, one obtains a numerical function 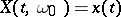 on
on 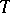 , called a realization (or sample function or, when
, called a realization (or sample function or, when 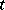 denotes time, a trajectory) of
denotes time, a trajectory) of 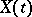 ;
; 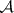 and
and 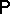 induce a
induce a 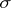 -algebra of subsets and a probability measure defined on it in the function space
-algebra of subsets and a probability measure defined on it in the function space 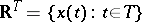 of realizations
of realizations 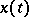 , whose specification can also be regarded as equivalent to that of the random function. The specification of a random function as a probability measure on a
, whose specification can also be regarded as equivalent to that of the random function. The specification of a random function as a probability measure on a 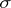 -algebra of subsets of the function space
-algebra of subsets of the function space 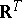 of all possible realizations
of all possible realizations 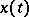 can be regarded as a special case of its general specification as a function of two variables
can be regarded as a special case of its general specification as a function of two variables  (where
(where 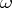 belongs to the probability space
belongs to the probability space 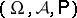 in which
in which 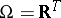 ), that is, elementary events (points
), that is, elementary events (points  in the given probability space) are identified at the outset with the realizations
in the given probability space) are identified at the outset with the realizations  of
of 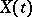 . On the other hand, it is also possible to show that any other way of specifying
. On the other hand, it is also possible to show that any other way of specifying 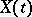 can be reduced to this form using a special determination of a probability measure on
can be reduced to this form using a special determination of a probability measure on 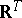 . In particular, Kolmogorov's fundamental theorem on consistent distributions (see Probability space) shows that the specification of the aggregate of all possible finite-dimensional distribution functions
. In particular, Kolmogorov's fundamental theorem on consistent distributions (see Probability space) shows that the specification of the aggregate of all possible finite-dimensional distribution functions 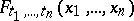 satisfying the above consistency conditions (1) and (2) defines a probability measure on the
satisfying the above consistency conditions (1) and (2) defines a probability measure on the 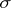 -algebra of subsets of the function space
-algebra of subsets of the function space  generated by the aggregate of cylindrical sets (cf. Cylinder set) of the form
generated by the aggregate of cylindrical sets (cf. Cylinder set) of the form 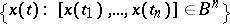 , where
, where  is an arbitrary positive integer and
is an arbitrary positive integer and 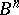 is an arbitrary Borel set of the
is an arbitrary Borel set of the  -dimensional space
-dimensional space 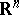 of vectors
of vectors  .
.
For references see Stochastic process.
Comments
References
| [a1] | J.L. Doob, "Stochastic processes" , Wiley (1953) |
| [a2] | M. Loève, "Probability theory" , Springer (1977) |
| [a3] | I.I. [I.I. Gikhman] Gihman, A.V. [A.V. Skorokhod] Skorohod, "The theory of stochastic processes" , 1 , Springer (1974) (Translated from Russian) |
| [a4] | A. Blanc-Lapierre, R. Fortet, "Theory of random functions" , 1–2 , Gordon & Breach (1965) (Translated from French) |
Random function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Random_function&oldid=13830