Flux of a vector field
From Encyclopedia of Mathematics
A concept in the theory of vector fields. The flux of a vector field 
through the surface 
is expressed, up to sign, by the surface integral
 |
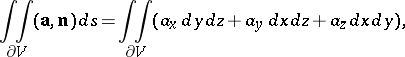where 
is the unit normal vector to the surface 
(it is assumed that the vector 
changes continuously over the surface 
). The flux of the velocity field of a fluid is equal to the volume of fluid passing through the surface 
per unit time.
Comments
The flux of a differential vector field 
(defined by the formula above) is related to the divergence of 
:
 |
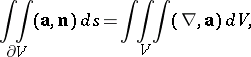where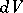 
is the volume element in 
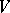and 
is the Hamilton operator,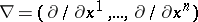 
. This equation is called the divergence theorem or also Green's theorem in space, cf. [a1] and Stokes theorem.
References
| [a1] | M. Spivak, "Calculus on manifolds" , Benjamin (1965) |
How to Cite This Entry:
Flux of a vector field. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Flux_of_a_vector_field&oldid=13812
Flux of a vector field. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Flux_of_a_vector_field&oldid=13812
This article was adapted from an original article by BSE-3 (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article