Completely-reducible matrix group

A matrix group 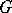over an arbitrary fixed field 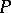, all elements of which may be reduced by simultaneous conjugation by some matrix over 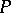to block-diagonal form, i.e. to the form

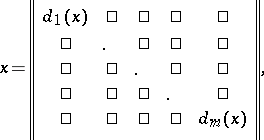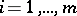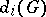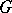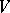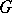where , , are square matrices, the remaining places being filled by zeros, and each matrix group is irreducible (cf. Irreducible matrix group). In the language of transformations, a group of linear transformations of a finite-dimensional vector space over a field is said to be completely reducible if any one of the following equivalent conditions is met: 1) Any subspace of which is -invariant has a -invariant direct complement (cf. Invariant subspace); 2) 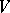is decomposable into the direct sum of minimal 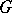-invariant subspaces; or 3) 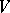is generated by the minimal -invariant subspaces. Every finite matrix group 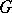over a field whose characteristic does not divide the order of 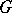is completely reducible. Every normal subgroup of a completely-reducible matrix group is itself completely reducible.

References

[1]	Yu.I. Merzlyakov, "Rational groups" , Moscow (1987) (In Russian)
[2]	M. Hall, "Group theory" , Macmillan (1959)

References

[a1]	W. Feit, "The representation theory of finite groups" , North-Holland (1982)
[a2]	C.W. Curtis, I. Reiner, "Representation theory of finite groups and associative algebras" , Interscience (1962)